Геометрия — это раздел математики, который занимается изучением геометрических фигур, в том числе основные понятия и определения, свойства и признаки точек, линий, углов, двумерных и трехмерных объектов, а также их размеров и взаимного расположения.
Основные геометрические фигуры — точка, прямая и плоскость. На рисунке:
- A, B, C, M — точки, обозначаются большой буквой,
- BC (или CB) и b — прямые, обозначается двумя большими или одной малой буквой латинского алфавита.
- α (альфа) — плоскость, обозначается тремя большими буквами латинского или одной малой буквой греческого алфавита.
Аксиома: через любые две точки плоскости можно провести прямую, и притом только одну.
- Две прямые называются пересекающимися, если они имеют общую точку.
- Две прямые называются параллельными, если они лежат в одной плоскости и не пересекаются.
Луч
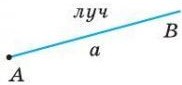
Луч — это часть прямой, который состоит из точки (начало луча) и всех ее точек, лежащих по одну сторону от данной точки. То есть, то часть прямой, ограниченная одной точкой. Он обозначается одной малой буквой (b) или двумя большими буквами (AB), где первой всегда записывается начало луча. При этом вторая точка может быть не отмечена на луче.
 |
Два луча называются дополнительными (противоположными), если они имеют общее начало и лежат на одной прямой. На рисунке изображены дополнительные лучи ОМ и ОK. Они дополняют друг друга до прямой. 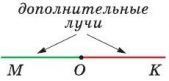
Отрезок
Отрезок — это часть прямой, ограниченная двумя точками. Точки, ограничивающие отрезок, принадлежат отрезку и называются концами отрезка, остальные точки отрезка — его внутренними точками. Обозначение: AB (или BA, или m).
Расстоянием между двумя точками называется длина отрезка, соединяющего эти точки.
Серединой отрезка называется точка, которая делит отрезок на два равных отрезка. На рисунке точка М — середина отрезка EF, то есть EM = MF.![]()
Ломаная
Ломаной называется геометрическая фигура, образованная отрезками, последовательно соединенными своими концами. На рисунке изображена ломаная ABCDEF. Указанные отрезки называются звеньями ломаной, а точки A, B, C, D, E и F — вершинами ломаной.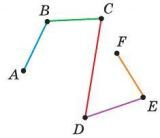
- Замкнутая ломаная — если начало ее первого звена совпадает с концом последнего.
- Простая ломаная — если она не имеет самопересечений и никакие два ее звена, кроме соседних, не имеют общих точек.
Геометрические фигуры
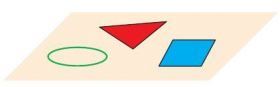
- Плоские (планиметрия) — все точки расположены на одной плоскости: треугольник, квадрат, прямоугольник, параллелограмм, ромб, трапеция, окружность и другие фигуры.
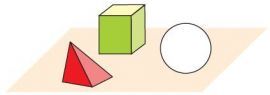
- Объемные (стереометрия) -не могут целиком располагаться в одной плоскости: многогранники (куб, пирамида, призма, параллелепипед и др.) и тела вращения (цилиндр, конус, шар и др.).
 |
 |
Углы
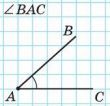
Угол — геометрическая фигура, образованная двумя лучами (сторонами угла), выходящими из одной точки (которая называется вершиной угла). На рисунке: точка A — вершина угла, лучи AB и AC— стороны угла. Обозначение: BAC (или ∠A — если понятно, о каком угле идет речь).
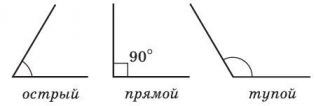
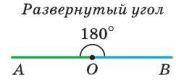
Виды углов: острый (меньше 90°), прямой (равен 90°) и тупой (больше 90°, но меньше 180°). Также выделяют развернутый угол (равен 180°).
 |
 |
Параллельные и перпендикулярные прямые
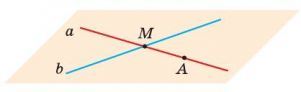
На плоскости две прямые могут либо пересекаться, либо не пересекаться.
 |
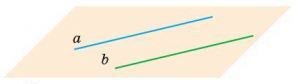 |
Прямые на плоскости, которые не пересекаются, называются параллельными. Если прямые а и b параллельны, то пишут а || b.
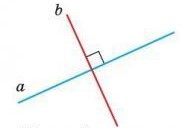
Две прямые, которые при пересечении образуют прямой угол, называются перпендикулярными прямыми. Если прямые а и b перпендикулярны, то пишут а ⊥ b. При пересечении двух перпендикулярных прямых образуются 4 прямых угла.
- Теорема. Через точку, лежащую на данной прямой, можно провести прямую, перпендикулярную этой прямой, и только одну.
- Теорема. Через точку, не лежащую на данной прямой, можно провести прямую, перпендикулярную этой прямой, и притом только одну.
Из двух последних теорем следует, что на плоскости через любую точку можно провести прямую, перпендикулярную данной прямой, и притом только одну.
Теорема (о двух прямых, перпендикулярных третьей). На плоскости две прямые, перпендикулярные третьей, параллельны между собой. 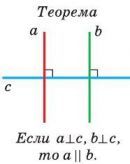
Аксиома и теорема
Свойства фигур формулируются в виде аксиом и теорем.
Аксиома — это утверждение, которое принимается без доказательства. Например: через любые две точки плоскости можно провести прямую, и притом только одну.
Теорема — это утверждение, которое требует доказательства. Теорема — верное утверждение, справедливость которой устанавливается путем логических рассуждений, которое называются доказательством. Доказательство каждой теоремы опирается на аксиомы и ранее доказанные теоремы. Например: на плоскости две прямые, перпендикулярные третьей прямой, параллельны между собой.