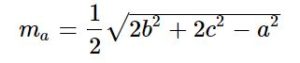Геометрия: свойства треугольника

Треугольник – это геометрическая фигура, которая состоит из трёх точек, не лежащих на одной прямой (вершин треугольника) и трёх отрезков с концами в этих точках (сторон треугольника).

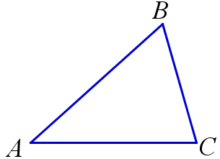На рисунке: Треугольник ABC;
A, B, C – вершины треугольника ABC;
AB, AC, BC – стороны треугольника ABC;
∠BAC, ∠ABC, ∠ACB – углы треугольника ABC.

Виды треугольников

Треугольник называется остроугольным, если все его углы острые.
Треугольник называется тупоугольным, если один из его углов тупой.
Треугольник называется прямоугольным, если один из его углов прямой. Стороны, прилежащие к прямому углу, называются катетами, противолежащая прямому углу – гипотенузой.
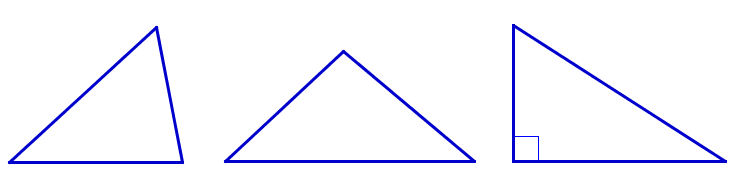
Равнобедренный треугольник— треугольник, у которого две стороны равны. Равные стороны называют боковыми сторонами, а третью – основанием равнобедренного треугольника.
Равносторонний или правильный треугольник – треугольник, у которого все стороны равны.
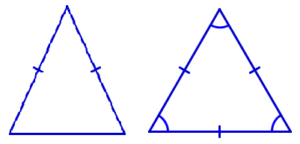
Равные треугольники – треугольники, у которых соответствующие стороны равны и соответствующие углы равны. Основные признаки равенства треугольников: по двум сторонам и углу между ними, по стороне и двум прилежащим к ней углам, по трем сторонам.

Свойства сторон треугольника

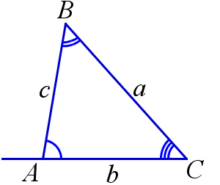
Сумма любых двух сторон треугольника больше его третьей стороны.
На рисунке: b+c>a, a+c>b, a+b>c.
Длина каждой стороны треугольника больше разности длин двух других сторон. На рисунке: |a-b| <c, |a-c|<b, |b-c|<a.

Свойства углов треугольника

Сумма углов треугольника равна 180°:
В треугольнике против большего угла лежит большая сторона, против большей стороны лежит больший угол.
Внешний угол треугольника равен сумме двух внутренних углов, с ним не смежных.

Свойства высоты треугольника

Высота треугольника — перпендикуляр, опущенный из любой вершины треугольника на противолежащую сторону или на продолжение стороны. На рисунке: BD – высота треугольника ABC.

Высоты треугольника пересекаются в одной точке, которая называется ортоцентром треугольника. На рисунке: H – ортоцентр треугольника ABC.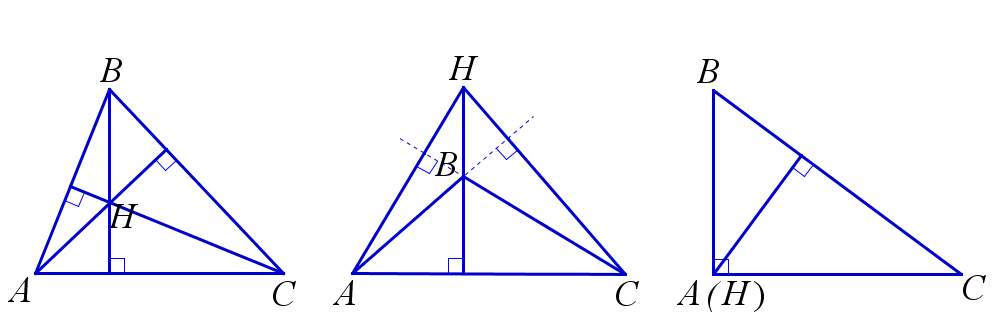

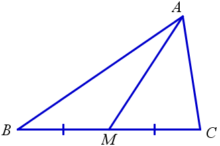
Свойства медианы треугольника

Медиана — это отрезок, соединяющий вершину треугольника с серединой противоположной стороны (AM).
— Она делит треугольник на два равновеликих (с равными площадями) треугольника.
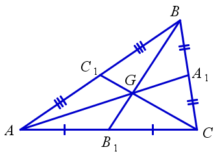
— Три медианы треугольника делят его на шесть равновеликих треугольников. Медианы треугольника пересекаются в одной точке и делятся точкой пересечения в отношении 2:1, считая от вершины треугольника. На рисунке: AG/GA1=BG/GB1=CG/GC1=2/1.

Формула медианы:

Свойства биссектрисы треугольника

Биссектрисой треугольника, проведённой из данной вершины, называется отрезок биссектрисы угла треугольника, соединяющий эту вершину с точкой на противолежащей стороне. На рисунке: AL – биссектриса треугольника ABC.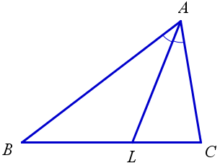

Свойство биссектрисы треугольника: Отношение отрезков, на которые биссектриса делит сторону треугольника, равно отношению прилежащих к этим отрезкам сторон треугольника. На рисунке: BL/CL=AB/AC.

Биссектрисы треугольника пересекаются в одной точке. Эта точка равноудалена от всех сторон треугольника и является центром окружности, вписанной в треугольник.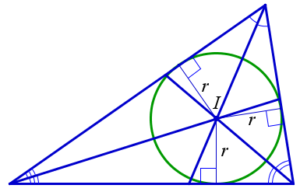

Формула нахождения длины биссектрисы: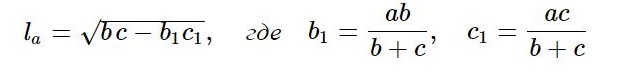

Средняя линия треугольника

Средняя линия треугольника – это отрезок, соединяющий середины двух сторон треугольника.
На рисунке: MN – средняя линия треугольника ABC.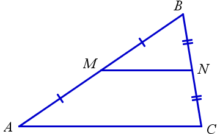

Средняя линия треугольника параллельна третьей стороне треугольника и равна её половине.
На рисунке: MN||AC,MN=AC/2.

Средние линии разбивают треугольник на четыре равных треугольника, подобных исходному с коэффициентом 1/2. Треугольник из средних линий называется срединным треугольником.
На рисунке: MNP – срединный треугольник треугольника ABC.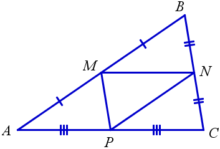

Равнобедренный треугольник

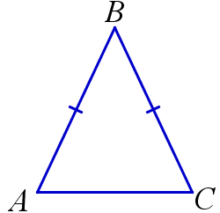Равнобедренный треугольник— треугольник, у которого две стороны равны. Равные стороны называют боковыми сторонами, а третью – основанием равнобедренного треугольника.

На рисунке:
△ABC равнобедренный;
AC – основание,
AB, BC – боковые стороны.

Свойства равнобедренного треугольника:

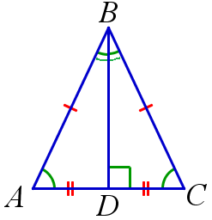В равнобедренном треугольнике углы при основании равны.
На рисунке: ∠BAC=∠BCA
В равнобедренном треугольнике медиана, проведённая к основанию, является и биссектрисой и высотой.
На рисунке: AD=DC, ∠ABD=∠CBD, BD⊥AC.

Признаки равнобедренного треугольника:

Если два угла треугольника равны, то этот треугольник равнобедренный. На рисунке: ∠BAC=∠CAB⇒AB=BC.
Если в треугольнике медиана и высота, проведённые к одной стороне, совпадают, то этот треугольник равнобедренный. На рисунке: AD=DC, BD⊥AC ⇒ AB=BC.
Если в треугольнике медиана и биссектриса, проведённые к одной стороне, совпадают, то этот треугольник равнобедренный. На рисунке: AD=DC, ∠ABD=∠CBD ⇒ AB=BC.
Если в треугольнике высота и биссектриса, проведённые к одной стороне, совпадают, то этот треугольник равнобедренный. На рисунке: BD⊥AC, ∠ABD=∠CBD ⇒ AB=BC.

Равносторонний треугольник

Все стороны равностороннего треугольника равны.
Все углы равностороннего треугольника равны 60°.
Каждая медиана равностороннего треугольника совпадает с биссектрисой и высотой.

Прямоугольный треугольник

Треугольник называется прямоугольным, если один из его углов прямой. Стороны, прилежащие к прямому углу, называются катетами, противолежащая прямому углу – гипотенузой.
На рисунке: △ABC прямоугольный; AC, BC – катеты, AB – гипотенуза.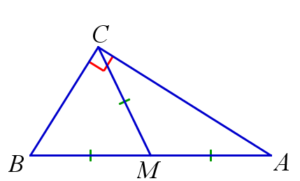

Медиана прямоугольного треугольника, проведённая к гипотенузе, равна половине гипотенузы.
На рисунке: ∠C=90∘,CM – медиана △ABC⇒AM=BM=CM.

Высота, проведённая к гипотенузе, делит прямоугольный треугольник на два треугольника подобных друг другу и исходному треугольнику. На рисунке: △ACH∽△CBH∽△ABC.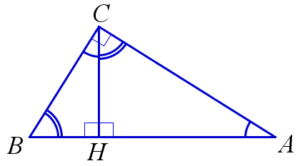

В прямоугольном треугольнике катет, лежащий напротив угла в 30∘, равен половине гипотенузы.
На рисунке: если ∠A=30∘⇔BC=AB/2.

Основные метрические соотношения в прямоугольном треугольнике:
Пусть в треугольнике ABC ∠C=90∘, a=BC, b=AC – катеты, c=AB – гипотенуза, h=CH – высота к гипотенузе, a1=BH, b1=AH – проекции катетов на гипотенузу. Тогда:

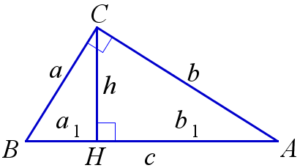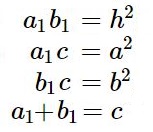В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов (Теорема Пифагора).В прямоугольном треугольнике гипотенуза всегда больше любого из катетов. Центром окружности, описанной около прямоугольного треугольника, является середина гипотенузы. Радиус описанной окружности прямоугольного треугольника равен половине гипотенузы: Радиус r окружности, вписанной в прямоугольный треугольник, может быть вычислен по формуле: r=(a+b−c)/2, где a и b – катеты треугольника, c – его гипотенуза.

Калькулятор для прямоугольного треугольника поможет вычислить все его характеристики: стороны, углы, периметр и площадь, радиус вписанной и описанной окружности.

Треугольник и окружность

Около любого треугольника можно описать окружность, и только одну. Центром окружности, описанной около треугольника, является точка пересечения серединных перпендикуляров к сторонам треугольника.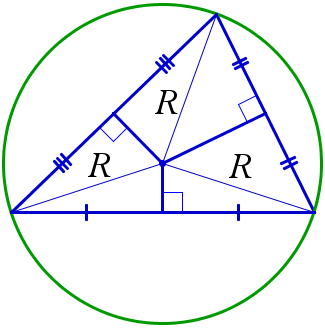

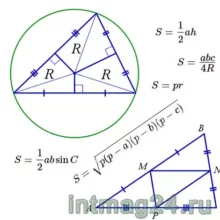
Радиус описанной окружности треугольника ABC может быть вычислен по формулам: 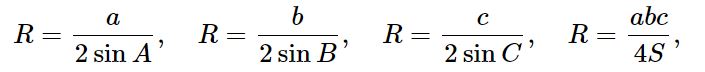где a, b и c – длины сторон треугольника ABC, S – его площадь.

В любой треугольник можно вписать окружность, и только одну. Центром вписанной окружности треугольника является точка пересечения биссектрис треугольника.

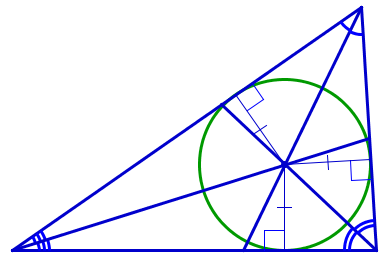Пусть a, b и c – длины сторон треугольника ABC и p=(a+b+c)/2 – его полупериметр. Тогда
— длины отрезков касательных из вершин A, B, C до точек касания вписанной окружности со сторонами треугольника равны p−a, p−b, p−c соответственно.

Радиус r вписанной окружности треугольника может быть вычислен по формуле: 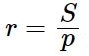где a, b и c – длины сторон треугольника, p=(a+b+c)/2 – его полупериметр, S – площадь треугольника.

Основные формулы:

Периметр: P=a+b+c

Площадь по стороне и высоте: площадь треугольника равна половине произведения стороны треугольника на высоту, проведённую к этой стороне.

Площадь по сторонам и углу между ними: площадь треугольника равна половине произведения двух его сторон на синус угла между ними. 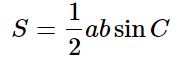или половине произведения катетов:

Площадь по формуле Герона (где p=(a+b+c)/2 – полупериметр, a, b, c – стороны треугольника):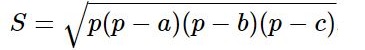

Площадь по трем сторонам и радиусу вписанной окружности (где p=(a+b+c)/2 – полупериметр треугольника, r — радиус вписанной окружности): Площадь по трем сторонам и радиусу описанной окружности: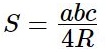

Стороны прямоугольного треугольника (Теорема Пифагора):

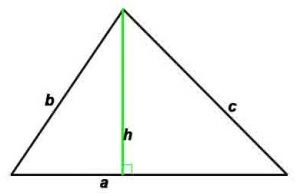где a,b, c — стороны (a,b –катеты , с – гипотенуза в случае прямоугольного треугольника)
h -высота, проведенная к противоположной стороне,
P-периметр, S-площадь, γ — угол между сторонами и r — радиус вписанной окружности, R — радиус описанной окружности

Для нахождения характеристик простого, равнобедренного или равностороннего треугольника, воспользуйтесь калькулятором для треугольника.

Чтобы вычислить все характеристики прямоугольного треугольника, воспользуйтесь калькулятором для прямоугольного треугольника.

Скачать программы, которые формируют задания на нахождение периметра и площади геометрических фигур, а также неизвестных характеристик (сторон, диагоналей и др.), в том числе для: квадрата, прямоугольника, треугольника, трапеции и другие.

Теорема Чевы

Пусть A1, B1, C1 – точки на прямых BC, AC и AB, содержащих стороны треугольника ABC. Прямые AA1, BB1 и CC1 пересекаются в одной точке тогда и только тогда, когда:

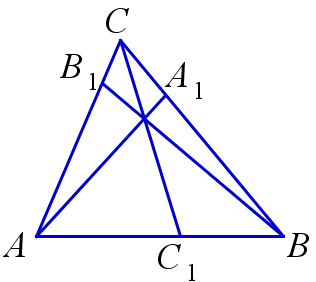
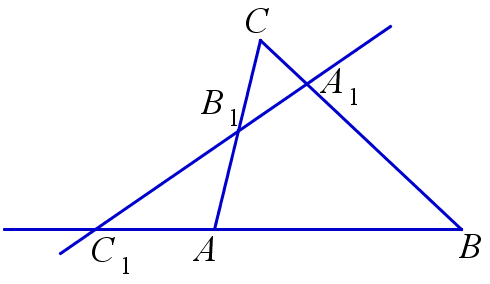
Теорема Менелая

Пусть A1, B1, C1 – точки на прямых BC, AC и AB, содержащих стороны треугольника ABC. Точки A1, B1 и C1 лежат на одной прямой тогда и только тогда, когда: