 Тела вращения (объемные геометрические фигуры) : определения, формулы периметра поверхности и площади. Виды: цилиндр, конус, шар, шаровой сектор, шаровой сегмент.
Тела вращения (объемные геометрические фигуры) : определения, формулы периметра поверхности и площади. Виды: цилиндр, конус, шар, шаровой сектор, шаровой сегмент.
Цилиндр
- Цилиндр — тело, ограниченное цилиндрической поверхностью с замкнутой направляющей и двумя параллельными плоскостями.
- Цилиндрическая поверхность — поверхность, образуемая однопараметрическим семейством параллельных прямых (образующих) и проходящими через точки некоторой кривой (направляющей).
- Основания цилиндра — плоские фигуры, образованные пересечением цилиндрической поверхности с двумя параллельными плоскостями, ограничивающими цилиндр.
- Высота цилиндра — расстояние между основаниями цилиндра.
Виды цилиндров
- Прямой — цилиндр, основания которого имеют центры симметрии (например, являются кругами или эллипсами), прямая между которыми перпендикулярна плоскостям этих оснований. Данная прямая называется осью цилиндра.
- Косой — цилиндр, основания которого имеют центры симметрии (например, являются кругами или эллипсами), отрезок между которыми не перпендикулярен плоскостям этих оснований.
- Круговой — цилиндр с окружностью в роли направляющей.
- Цилиндр вращения (или прямой круговой) — цилиндр, который можно получить вращением (то есть тело вращения) прямоугольника вокруг одной из его сторон, содержащая которую прямая в таком случае будет осью этого цилиндра и его осью симметрии.
- Эллиптический, параболический и гиперболический – цилиндр, основания которого являются эллипсами, параболами или гиперболами. Последние два имеют бесконечный объём.
- Равносторонний — цилиндр вращения, диаметр основания которого равен его высоте.
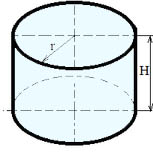 Формулы для цилиндра:
Формулы для цилиндра:
Объем цилиндра: V=π∙R2∙h или V=So∙h
Поверхность цилиндра: S= 2∙So + Sбок или S= 2∙π∙R2 + 2∙π∙R∙h
Площадь основания: So= 2∙π∙R2
Площадь боковой поверхности: Sбок=2∙π∙R∙h
Где: V — объем цилиндра, R — радиус цилиндра, h — высота цилиндра, So — площадь основания цилиндра, π = 3.141592.
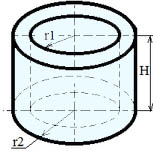 Формулы для полого цилиндра:
Формулы для полого цилиндра:
Объем цилиндра: V = π ∙ h ∙ (r22 — r12) где r2 > r1
Площадь боковой поверхности: Sбок = 2 ∙ π ∙ h ∙ (r1 + r2)
Где: V — объем цилиндра, R — радиус цилиндра, h — высота цилиндра, So — площадь основания цилиндра, π = 3.141592.
Конус
- Конус – поверхность, образованная в пространстве множеством лучей (образующих конуса), соединяющих все точки некоторой плоской кривой (направляющей конуса) с данной точкой пространства (вершиной конуса).
- Боковая поверхность конуса — объединение образующих конуса; образующая поверхность конуса является конической поверхностью.
- Высота конуса — отрезок, опущенный перпендикулярно из вершины на плоскость основания (а также длина такого отрезка).
- Угол раствора конуса — угол между двумя противоположными образующими (угол при вершине конуса, внутри конуса).
- Конусность — соотношение высоты и диаметра основания конуса.
Типы конусов
- Прямой — конус, основание которого имеет центр симметрии (например, является кругом или эллипсом) и ортогональная проекция вершины конуса на плоскость основания совпадает с этим центром. Прямая, соединяющая вершину и центр основания, называется осью конуса.
- Косой (или наклонный) — конус, у которого ортогональная проекция вершины на основание не совпадает с его центром симметрии.
- Круговой — конус, основание которого является кругом.
- Конус вращения или прямой круговой конус (часто под конусом подразумевают именно его) — конус, который можно получить вращением (то есть тело вращения) прямоугольного треугольника вокруг прямой, содержащей катет треугольника (эта прямая является осью конуса).
- Эллиптический, параболический и гиперболический — конус, опирающийся на эллипс, параболу или гиперболу. Последние два имеют бесконечный объем.
- Усечённый или конический слой — часть конуса, лежащая между основанием и плоскостью, параллельной основанию и находящейся между вершиной и основанием.
- Равносторонний — конус вращения, образующая которого равна диаметру основания.
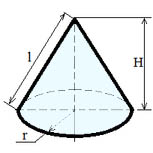 Формулы для конуса:
Формулы для конуса:
Объем конуса: V = 1/3·π·R2·h или V=1/3·So·h
Поверхность конуса: S=So+Sбок или S=π∙R2+π∙R∙h
Площадь основания: So=π∙R2
Площадь боковой поверхности: Sбок=π∙R∙l
Образующая: l=√(R2+h2)
Где: V — объем конуса, So — площадь основания, R — радиус основания, h — высота конуса, l — образующая, π=3.141592.
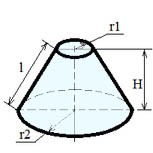 Формулы для усеченного конуса:
Формулы для усеченного конуса:
Объем конуса: V=1/3·π·(r12+r22+r1·r2)·h
Площадь боковой поверхности: Sбок=π∙(r1+r2)∙l
Где: r1 — радиус нижнего основания усеченного конуса; r2 — радиус верхнего основания усеченного конуса; l — образующая усеченного конуса, π=3.141592.
Шар
- Шар — это тело ограниченное шаровой поверхностью.
- Шаровая (сферическая) поверхность – это геометрическое место точек пространства, равноудаленных от одной точки — центра шара. Радиус и диаметр определяют также, как и для окружности.
- Все плоские сечения шара — круги. Наибольший круг получается в сечении шара плоскостью, проходящей через центр. Такой круг делит шар пополам. Радиус большого круга равен радиусу шара. Через две точки шара, лежащие на концах одного диаметра, можно провести бесчисленное множество больших кругов — меридианы. Через две точки, не лежащие на концах диаметра шара можно провести только один большой круг.
- Шаровой сектор — это часть шара, ограниченная кривой поверхностью шарового сегмента и конической поверхностью основанием которой служит основание сегмента, а вершиной — центр шара.
- Шаровой (сферический) сегмент — часть шара, осекаемая от него какой-нибудь плоскостью. Основание шарового сегмента – круг. Высота шарового сегмента — длина перпендикуляра от поверхности шара до основания. Вершина шарового сегмента — точка пересечения высоты шарового сегмента с поверхностью шара.
-
Шаровой слой — это часть шара, заключенная между двумя секущими параллельными плоскостями. Шаровой пояс или Шаровая зона — кривая поверхность шарового слоя. Круги — основания шарового пояса. Расстояние между основаниями — высота шарового слоя.
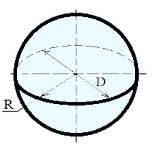 Формулы для шара:
Формулы для шара:
Объем шара: V = 4/3 ·π· R3 или V=1/6 ·π · D3
Площадь поверхности сферы: S= 4 ·π· R2 или S=π · D2
Площадь основания: So=π∙R2
Где: R — радиус шара, π = 3.141592.
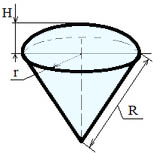 Формулы для шарового сектора:
Формулы для шарового сектора:
Высота конуса: hконуса=R2−r2
Высота сегмента: hсегмента= R−R2−r2
Площадь поверхности шарового сектора: Sсектора= Sсегмента+ Sконуса
или Sсектора= 2∙π∙R∙hсегмента + π∙R∙rили Sсектора=2∙π∙ R ∙(R−R2−r2) + π∙R∙r
Объем шарового сектора: V = 2/3∙(π∙R2∙h) или V = 1/3∙( R∙S)
Где: R — радиус шара, r — радиус сегмента, π = 3.141592.
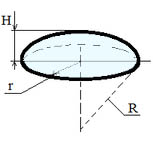 Формулы для шарового сегмента:
Формулы для шарового сегмента:
Площадь поверхности шарового сегмента : S = 2∙π∙R∙h
Объем шарового сегмента : V = (π ·H2 (R -1/3 ·h)
Где: R — радиус шара, r — радиус сегмента, h= высота шарового сегмента, π = 3.141592.
Также на сайте описаны многогранники, в том числе: определения и формулы.
