Геометрия: свойства ромба

Ромб — это параллелограмм, у которого все стороны равны. При этом трапеция обладает всеми свойствами четырехугольника и параллелограмма. Поэтому запоминать надо свойства, которые характерны для ромба.

Свойства ромба:

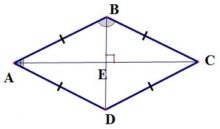
1. Противоположные углы равны. На рисунке: ∠BAC=∠DAC=∠BCA=∠DCA, ∠ABD=∠CBD=∠ADB=∠CDB.
2. Диагонали точкой пересечения делятся пополам. На рисунке: точка E.
3. Диагонали ромба пересекаются под прямым углом. На рисунке: AC⊥BD
4. Диагонали ромба являются биссектрисами его углов.

Признаки ромба:

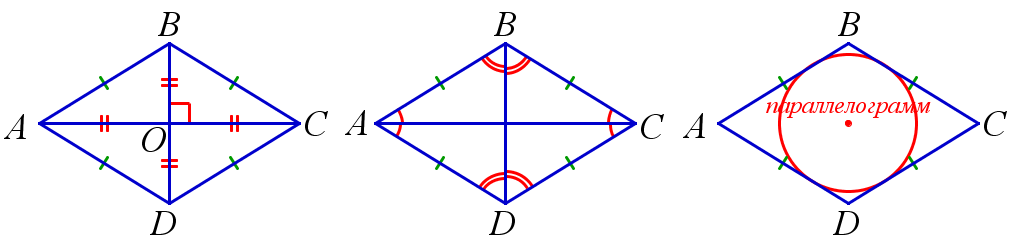
1. Если диагонали четырёхугольника перпендикулярны и делятся точкой пересечения пополам, то этот четырёхугольник – ромб. На рисунке: AC⊥BD,AO=CO,BO=DO
2. Если диагонали четырёхугольника лежат на биссектрисах его углов, то этот четырёхугольник – ромб. На рисунке: ∠BAC=∠DAC,∠BCA=∠DCA∠ABD=∠CBD,∠ADB=∠CDB.
3. Если четырёхугольник — это параллелограмм и в него можно вписать окружность, то этот четырёхугольник – ромб. На рисунке: AB||CD,BC||AD,ABCD – описанный.

Ромб и окружность

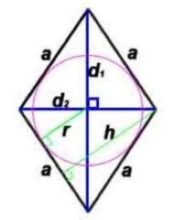
В ромб можно вписать окружность. Центром этой окружности является точка пересечения диагоналей ромба.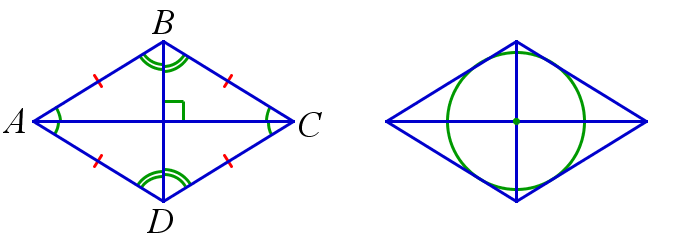

Радиус окружности, вписанной в ромб, можно найти по формуле: или где: a — длина стороны, d₁, d₂ –диагонали.

Четырёхугольник можно описать окружностью, если сумма его противолежащих углов равна 180°. Таким образом, ромб, вписанный в окружность – это квадрат. Центр окружности совпадает с точкой пересечения диагоналей.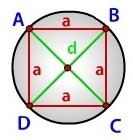

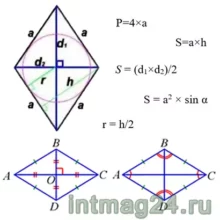
Основные формулы для ромба:

 Периметр: Площадь по стороне и высоте: Площадь по диагоналям: Радиус окружности, вписанной в ромб: или Площадь по стороне и радиусу вписанной окружности:

Площадь по стороне и углу:

где a — длина стороны, d₁, d₂ –диагонали, P-периметр, S-площадь,
h -высота, проведенная к противоположной стороне
α — угол между сторонами ромба.