 Логарифм — это показатель степени, то есть в какую степень надо возвести число, которое стоит в основании, чтобы получить число в выражении логарифма.
Логарифм — это показатель степени, то есть в какую степень надо возвести число, которое стоит в основании, чтобы получить число в выражении логарифма.
Например, log28 означает: в какую степень надо возвести 2, чтобы получить 8
Получаем: log28=3 (то есть 23=8)
Читается: как логарифм 8 по основанию 2 равен 3.
Понятие логарифма
Логарифм по основанию a от аргумента b — это степень, в которую надо возвести число a, чтобы получить число b. 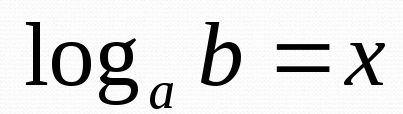
где a — основание, b — аргумент, x — чему равен логарифм.
Область допустимых значений (ОДЗ логарифма)
ОДЗ (область допустимых значений) логарифма – это множество всех действительных чисел, для которых определена данная функция.
ОДЗ логарифма:
Таким образом, область допустимых значений логарифма (ОДЗ логарифма) состоит из трёх условий:
- Число x может быть любым, так как степень может быть любой – отрицательной, рациональной, иррациональной и т.д.
- Основание (a) — это всегда положительное число.
- Основание (a) не может быть равно единице, поскольку единица в любой степени все равно остается единицей.
- Аргумент (b) — всегда положительное число.
Виды логарифмов
- Логарифм по произвольному основанию — это логарифм, вычисленный для произвольного положительного числа a, отличного от 1. Логарифм по произвольному основанию обозначается как logₐb, где a — основание логарифма, а b — аргумент логарифма.
- Десятичный логарифм — логарифм, у которого основание равно 10.
Обозначается lg (log10b). - Натуральный логарифм — логарифм, у которого основание равно e, где e— иррациональная константа, приблизительно равная 2,718 (более точно e=2,718281828459).
Обозначается ln (logeb).
Как посчитать логарифм
- Чтобы было проще, постарайтесь представить основание и аргумент в виде степеней с одинаковым основанием.
- Все десятичные дроби нужно перевести в обыкновенные дроби.
- Разобраться, в какую степень нужно возвести основание, чтобы получить аргумент.
Примеры логарифмов
Примеры, где основание равно 2
Определим, в какую степень нужно возвести 2, чтобы получить аргумент:
log2(4)=2, log2(8)=3, log2(16)=4, log2(32)=5, log2(64)=6 .
Примеры, где основание равно 3
Определим, в какую степень нужно возвести 3, чтобы получить аргумент:
log3(9)=2, log3(27)=3, log3(81)=4, log3(243)=5.
Пример, в котором логарифм является иррациональным числом
Определим, в какую степень нужно возвести 3, чтобы получить 10:
log3(10)=2,095903. Здесь получится иррациональное число, которое можно вычислить с помощью специального калькулятора или онлайн калькулятора логарифмов. Если рассуждать логически, то результат будет лежать на промежутке: 32<10<33.
Пример с отрицательным логарифмом
log5(1/125)=?
Определим, в какую степень нужно возвести 5, чтобы получить 1/125: 1/125 = 1/53= 5-3.
Получаем ответ: log5(1/125)= 5-3.
Пример с дробным логарифмом
log64(4)=?
Представим число 64 в виде числа 2 в степени: 64 = 26.
Определим, в какую степень нужно возвести 26, чтобы получить 4 (или 22).
Чтобы получить 22, нужно 26 умножить на степень 1/3.
Получаем: log64(4)=1/3
Пример с нулевым логарифмом
log8(1)=?
Представим числа 8 и 1 в виде числа 2 в степени: 8= 23, 1= 20.
Определим, в какую степень нужно возвести 23, чтобы получить 20.
Чтобы получить 20, нужно (23)0 = 23*0 .
Получаем: log8(1)=0
Пример с десятичным логарифмом
log10(100)=2 или lg(100)=2,
log10(1000)=3 или lg(1000)=3,
log10(10000)=4 или lg(10000)=4.
Онлайн калькуляторы для вычисления логарифмов
- Калькулятор логарифмов онлайн (для всех типов логарифмов)
- Калькулятор десятичного логарифма
- Калькулятор натурального логарифма

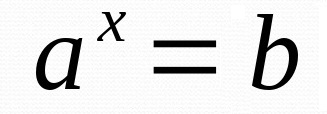
Наконец то все понятно про логарифмы!!! спс