Основные свойства логарифмов

Основные свойства логарифмов необходимо знать для того, чтобы решать различные задачи. По сути, логарифмы — это те же числа, которые можно складывать, вычитать, преобразовывать и т.д. Но они заданы по своим правилам, без знания которых не решается ни одна серьезная логарифмическая задача.

Частные случаи логарифмов

Логарифм единицы по любому положительному, отличному от 1, основанию равен нулю. Это возможно потому, что из любого действительного числа можно получить 1 только возведя его в нулевую степень.

Логарифм единицы равен нулю, так как a⁰=1 для любого a, удовлетворяющего условиям a>0 и a≠1.

Логарифм от произведения – это сумма логарифмов.

Примеры:
log₃(12) = log₃(3*4) = log₃(3) + log₃(4) = 1 + log₃(4)
log₃(2,7) + log₃(10) = log₃(2,7*10) = log₃(27) = 3

Логарифм от частного – это разность логарифмов.

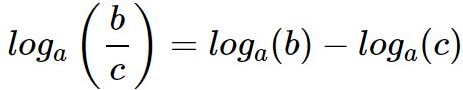Пример: log₇(98) — log₇(2) = log₇(98/2) = log₇(49) = 2.

Свойства степени

Логарифм степени равен произведению показателя степени на логарифм модуля основания этой степени.

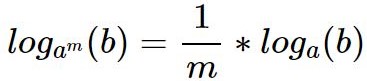
Пример: log₄(9) = log₂(3)

Переход к другому основанию

Формула перехода к новому основанию позволяет переходить к работе с логарифмами, имеющими «удобное» основание. Например, с ее помощью можно перейти к натуральным или десятичным логарифмам, чтобы можно было вычислить значение логарифма по таблице логарифмов.

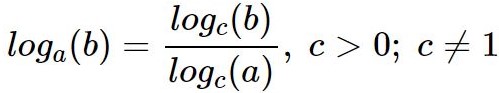
Пример: log₄(5) = log₇(5)/ log₇(4)

Частный случай формулы перехода к новому основанию

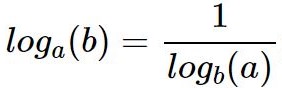
Пример: log₄(5) = 1/log₅(4)

Логарифмическое тождество

Онлайн калькуляторы для вычисления логарифмов

Калькулятор натурального логарифма