График логарифмической функции logax можно построить исходя из того, что функция обратна показательной функции y=ax. Поэтому можно построить график показательной функции, после чего отобразить его симметрично относительно прямой.
Логарифмической функцией называется функция вида y = logax. Она определена при a > 0, a ≠1, x > 0. Область значений логарифмической функции E = (-∞; +∞).
Итак, логарифмическая функция является обратной для показательной функции (это следует из определения логарифма), поэтому их графики симметричны относительно прямой y = x.
График логарифма
Область определения логарифмической функции
Область определения логарифмической функции — это множество всех положительных чисел.
Это следует из определения логарифма, так как выражение logax имеет смысл только при x > 0.
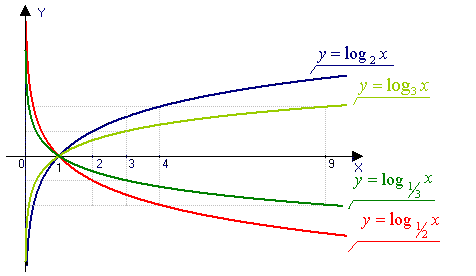
Построение графика функции логарифма
- График любой логарифмической функции проходит через точку (1; 0)
- При 0 < a < 1 функция строго убывает. Если 0 < a < 1, то функция y = logax принимает положительные значения при 0 < x < 1, отрицательные — при x > 1.
- При a > 1 функция строго возрастает. Если a > 1, то функция y = logax принимает положительные значения при x > 1, отрицательные — при 0 < x < 1.
Множество значений логарифмической функции
Множество значений логарифмической функции — множество всех действительных чисел.
Это следует из того, что для любого действительного числа b есть такое положительное число x, что logax = b, т.е. уравнение logax = b имеет корень. Такой корень существует и равен x = ab, так как logaab = b.
Онлайн калькуляторы для вычисления логарифмов
- Калькулятор логарифмов онлайн (для всех типов логарифмов)
- Калькулятор десятичного логарифма
- Калькулятор натурального логарифма
Также по теме:
Для освоения темы может понадобиться:
- Степень с натуральным показателем
- Степень с целым показателем
- Степень с целым отрицательным показателем
- Степень с дробным показателем
Инструкция: как скачать и запустить программу Excel