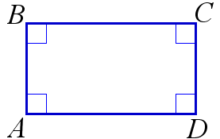
Прямоугольник — четырехугольник, у которого все углы прямые. Прямоугольник является частным случаем для четырехугольника, параллелограмма и ромба, поэтому обладает всеми их свойствами.
Свойства прямоугольника:
Диагонали прямоугольника равны и делятся точкой пересечения пополам.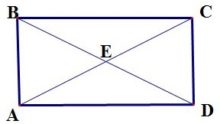 
Прямоугольник и окружность
Около любого прямоугольника можно описать окружность с центром в точке пересечения его диагоналей и радиусом, который равен половине диагонали.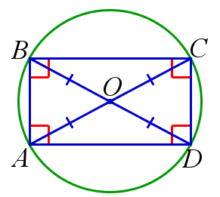 
В четырёхугольник можно вписать окружность, если суммы его противолежащих сторон равны. Таким образом, если в прямоугольник можно вписать окружность, то это – квадрат.
Центр вписанной в четырёхугольник окружности является точкой пересечения биссектрис всех четырёх углов этого четырёхугольника.
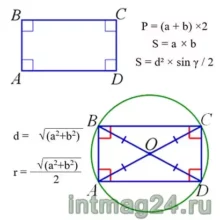
Основные формулы:
Периметр: 
Площадь по сторонам: 
Площадь по диагонали и углу между ними: 
Стороны и диагональ связаны соотношением (теорема Пифагора):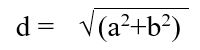 
Радиус описанной окружности (теорема Пифагора):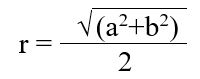 
где: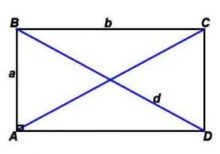
a, b — длины сторон прямоугольника,
d-диагональ,
P-периметр,
S-площадь,
γ – угол между диагоналями.
Калькулятор для прямоугольника поможет вычислить все характеристики прямоугольника (стороны, диагонали, периметр, площадь, радиус описанной окружности) по известным величинам.
Калькулятор для вычисления площади прямоугольника и квадрата вычисляет площадь данных фигур и работает в разных направлениях.
 |
Скачать программы, которые формируют задания на нахождение периметра и площади геометрических фигур, а также неизвестных характеристик (сторон, диагоналей и др.), в том числе для: квадрата, прямоугольника, треугольника, трапеции и другие. |