Параллелограмм – четырехугольник, у которого противолежащие стороны попарно параллельны.
Частными случаями параллелограмма являются прямоугольник, квадрат и ромб.
При этом параллелограмм обладает всеми свойствами четырехугольника. Поэтому запоминать надо свойства, которые характерны для параллелограмма.
Определения:
Высота параллелограмма (h) — это перпендикуляр, проведённый из вершины параллелограмма к противоположной стороне.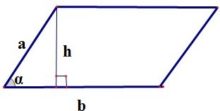
Частными случаями параллелограмма являются ромб, прямоугольник и квадрат.
Свойства углов и сторон параллелограмма
➜ Сумма углов параллелограмма равна 360°
➜ Сумма любых двух соседних углов параллелограмма равна 180°.
На рисунке: ∠A+∠B=180∘,∠A+∠D=180∘,∠C+∠B=180∘,∠C+∠D=180∘.
➜ У параллелограмма противоположные углы равны.
На рисунке: ∠A=∠C,∠B=∠D.
➜ У параллелограмма противоположные стороны параллельны и равны.
На рисунке: AB||CD и BC||AD; AB=CD,BC=AD.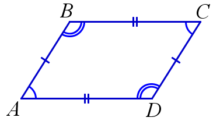
Диагонали параллелограмма
➜ Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам.
На рисунке: AO=CO,BO=DO.
➜ Каждая диагональ делит параллелограмм на два равных треугольника.
➜ Две диагонали параллелограмма делят его на четыре равновеликих треугольника (равны площади всех 4-х треугольников).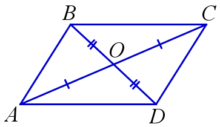
➜ Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон.
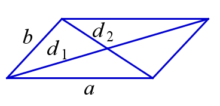
Признаки параллелограмма
1) Если в четырёхугольнике противоположные стороны попарно равны, то этот четырёхугольник – параллелограмм. На рисунке: AB=CD,BC=AD.
2) Если в четырёхугольнике противоположные углы попарно равны, то этот четырёхугольник – параллелограмм. На рисунке: ∠A=∠C,∠B=∠D.
3) Если в четырёхугольнике две противоположные стороны параллельны и равны, то этот четырёхугольник – параллелограмм. На рисунке: AB=CD,AB||CD.
4) Если в четырёхугольнике диагонали точкой пересечения делятся пополам, то этот четырёхугольник – параллелограмм. На рисунке: AO=CO,BO=DO.
Параллелограмм и окружность
В четырёхугольник можно вписать окружность, если суммы его противолежащих сторон равны. Таким образом, если в параллелограмм можно вписать окружность, то это – ромб.
Центр вписанной в четырёхугольник окружности является точкой пересечения биссектрис всех четырёх углов этого четырёхугольника.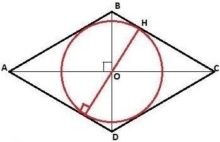
Четырёхугольник можно описать окружностью, если сумма его противолежащих углов равна 180°. Таким образом, параллелограмм, вписанный в окружность – это прямоугольник. Центр окружности совпадает с точкой пересечения диагоналей.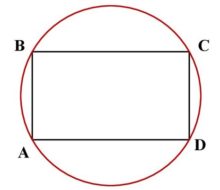
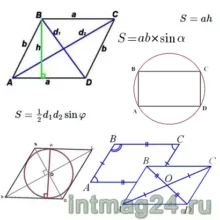
Основные формулы:
Стороны и диагональ связаны соотношением:
Периметр параллелограмма: 
Площадь параллелограмма можно найти по трём формулам.
1. Площадь параллелограмма равна произведению его стороны на высоту, проведённую к этой стороне.
 |
 |
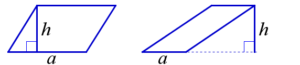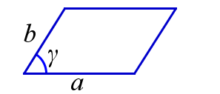
2. Площадь параллелограмма равна произведению двух смежных (соседних) сторон на синус угла между ними.
 |
 |
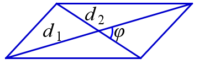
3. Площадь параллелограмма равна половине произведения его диагоналей на синус угла между ними.
 |
 |
Также см. Калькулятор для расчета площади параллелограмма и ромба
Комментарий:
- a, b — длины сторон,
- d1, d2 –диагонали,
- P-периметр,
- S-площадь,
h-высота, проведенная к противоположной стороне - α — угол между сторонами параллелограмма,
- γ — угол между диагоналями параллелограмма (острый).