Квадрат– прямоугольник, у которого все стороны равны. Квадрат является правильным четырёхугольником, у которого все углы равны и все стороны равны.
Квадрат — это частный случай четырехугольника, параллелограмма, прямоугольника и ромба, поэтому квадрат также обладает всеми их свойствами.
Свойства квадрата
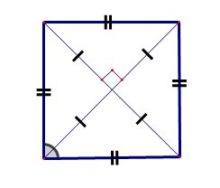
➜ Все стороны квадрата равны;
➜ Все углы равны и составляют 90°;
➜ Диагонали квадрата равны и перпендикулярны;
➜ Диагонали квадрата являются биссектрисами углов.
Признаки квадрата
1) Если четырёхугольник является прямоугольником и ромбом, то он – квадрат.
2) Если у прямоугольника две смежные стороны равны, то он – квадрат.
3) Если диагональ прямоугольника является биссектрисой его углов, то он – квадрат.
4) Если у ромба есть прямой угол, то он – квадрат.
5) Если диагонали ромба равны, то он – квадрат.
Основные формулы
Периметр:
Площадь по стороне квадрата. Площадь квадрата равна квадрату его стороны:
Площадь по диагоналям квадрата. Площадь квадрата равна половине произведения диагоналей:
Сторона и диагональ связаны соотношениями:
 |
 |
где: P-периметр, S-площадь квадрата, a-сторона, d-диагональ.
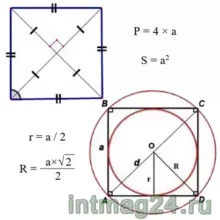
Квадрат и окружность
➜ Вокруг квадрата можно описать окружность.
➜ В квадрат можно вписать окружность.
У квадрата центры вписанной и описанной окружностей совпадают и находятся в точке пересечения его диагоналей.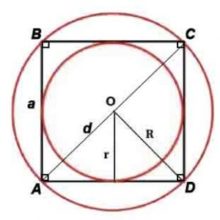 
Радиус описанной окружности:
 |
или |  |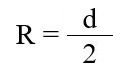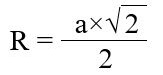
Радиус вписанной окружности: 
Калькулятор для квадрата поможет вычислить все характеристики квадрата (сторона, диагональ, периметр, площадь, радиус вписанной и описанной окружности) по одной из известных величин.
Калькулятор для вычисления площади прямоугольника и квадрата вычисляет площадь данных фигур и работает в разных направлениях.
 |
Скачать программы, которые формируют задания на нахождение периметра и площади геометрических фигур, а также неизвестных характеристик (сторон, диагоналей и др.), в том числе для: квадрата, прямоугольника, треугольника, трапеции и другие. |