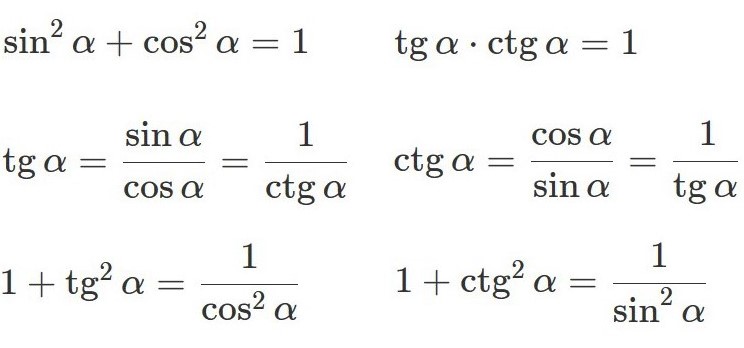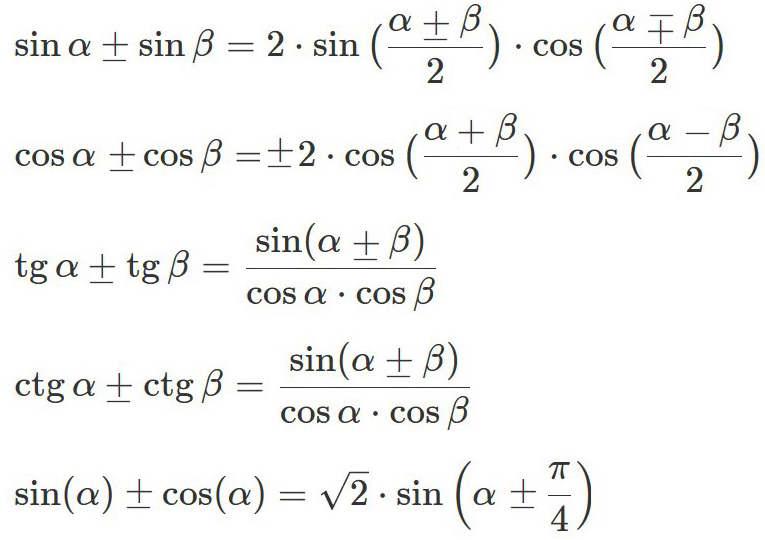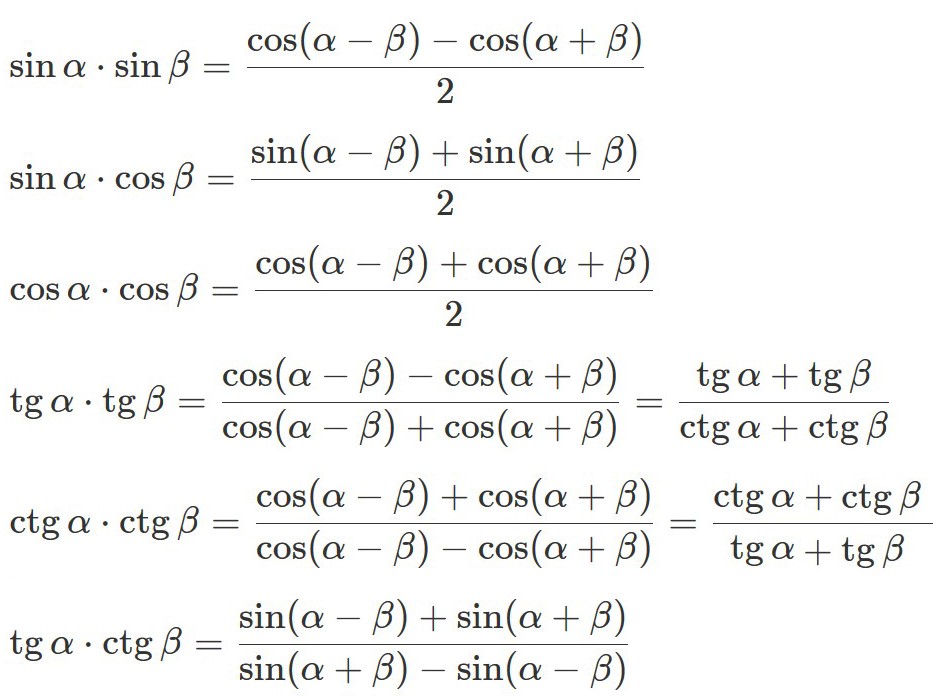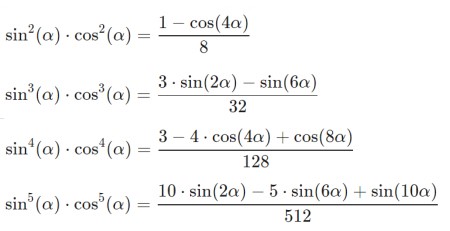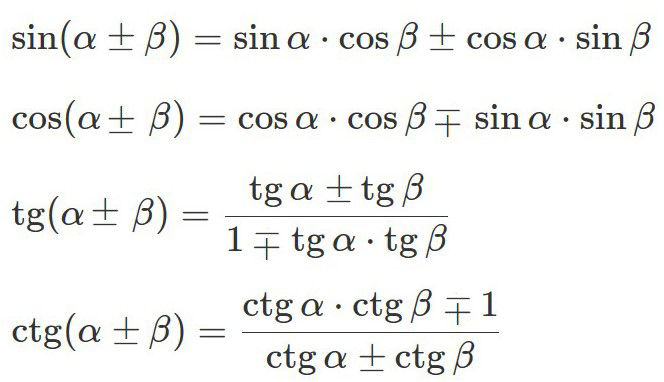Тригонометрия (определения и основные формулы) являются одной из базовых тем геометрии. Соотношения между основными тригонометрическими функциями (синусом, косинусом, тангенсом и котангенсом) задаются тригонометрическими формулами. А так как связей между тригонометрическими функциями достаточно много, то этим объясняется и обилие тригонометрических формул. Одни формулы связывают тригонометрические функции одинакового угла, другие – функции кратного угла, третьи – позволяют понизить степень, четвертые – выразить все функции через тангенс половинного угла, и т.д.
В этой статье по порядку перечислены все основные тригонометрические формулы, которых достаточно для решения подавляющего большинства задач тригонометрии. Для удобства запоминания и использования будем группировать их по назначению, и заносить в таблицы.
Определение
|
Прямые тригонометрические функции |
sin |
Синус угла в прямоугольном треугольнике – это отношение противолежащего катета к гипотенузе. |
cos |
Косинус угла в прямоугольном треугольнике – это отношение прилежащего катета к гипотенузе. |
|
| Производные тригонометрические функции |
tg |
Тангенс угла в прямоугольном треугольнике– это отношение противолежащего катета к прилежащему. |
ctg |
Котангенс угла в прямоугольном треугольнике – это отношение прилежащего катета к противолежащему. |
|
| Другие тригонометрические функции
|
sec |
Секанс угла в прямоугольном треугольнике — отношение гипотенузы к прилежащему катету |
cosec |
Косеканс угла в прямоугольном треугольнике — отношение гипотенузы к противолежащему катету. |
Тригонометрия: основные тригонометрические формулы
Основные тригонометрические тождества
Задают связь между синусом, косинусом, тангенсом и котангенсом одного угла. Они позволяют выразить одну тригонометрическую функцию через другую.
Формулы суммы и разности тригонометрических функций
Предназначены для упрощения тригонометрических выражений. Они используются при решении тригонометрических уравнений, так как позволяют раскладывать на множители, сумму и разность синусов и косинусов.
Формулы произведения тригонометрических функций
Предназначены для упрощения тригонометрических выражений. Они используются при решении тригонометрических уравнений, так как позволяют раскладывать на множители, сумму и разность синусов и косинусов.
Формулы произведения тригонометрических функций в степени
Формулы сложения и вычитания аргументов
Формулы двойного, половинного и тройного углов
Формулы понижения степени
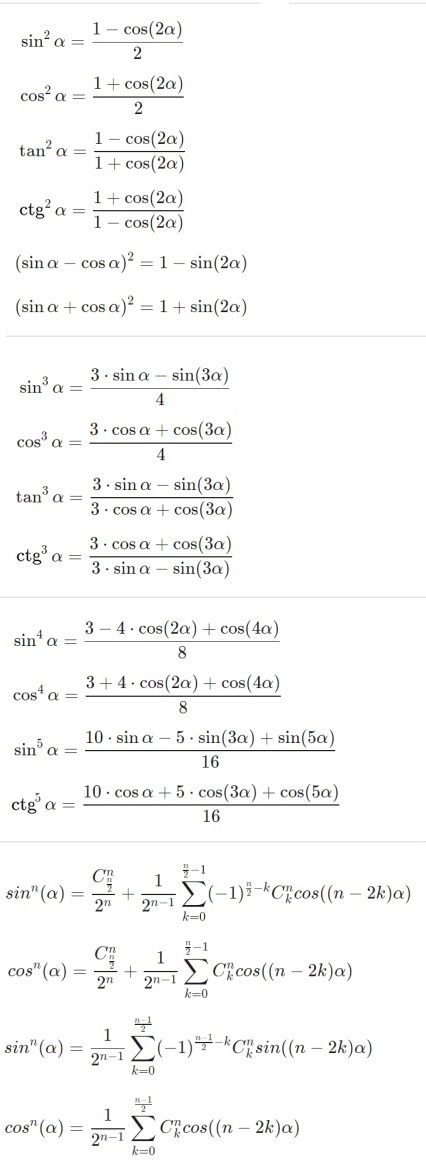Тригонометрия: основные значения
| Угол | 0° | 30° | 45° | 60° | 90° | 180° | 270° | 360° |
|---|---|---|---|---|---|---|---|---|
| Синус sin | 0 | 1/2 | √2/2 | √3/2 | 1 | 0 | -1 | 0 |
| Косинус cos | 1 | √3/2 | √2/2 | 1/2 | 0 | -1 | 0 | 1 |
| Тангенс tan | 0 | 1/√3 | 1 | √3 | — | 0 | — | 0 |
| Котангенс cot | — | √3 | 1 | 1/√3 | 0 | — | 0 | — |
| Секанс sec | 1 | 2√3/3 | √2 | 2 | — | -1 | — | 1 |
| Косеканс cosec | — | 2 | √2 | 2√3/3 | 1 | — | -1 | — |
| Угол | 0 | π/6 | π/4 | π/3 | π/2 | π | 3π/2 | 2π |
Также может понадобиться:
- Таблица Брадиса: как пользоваться
- Таблица Брадиса для синуса и косинуса
- Таблица Брадиса для тангенса и котангенса
- Таблица для секанса и косеканса
- Тригонометрический калькулятор онлайн (для нахождения синуса, косинуса, тангенса, котангенса, секанса и косеканса)
- Как найти синус, косинус, тангенс, котангенс, секанс и косеканс угла