Степень с целым показателем

Степень с целым показателем — это степень, показателем которой является любое целое число: натуральное, нулевое или отрицательное целое. В этой статье мы подробно разберем, как производить вычисления и преобразовывать выражения, содержащие разные виды показателей. Вы узнаете, что такое степень с целым показателем, как она работает для положительных и отрицательных чисел, и научитесь применять правила действий на практике. Материал сопровождается наглядными примерами, которые помогут вам быстро освоить тему.

Степень с натуральным показателем

Этот вид степени также является степенью с целым показателем, поскольку натуральные числа относятся к целым числам.
Степень с натуральным показателем — это произведение из нескольких одинаковых множителей.
Например: 2 × 2 × 2 = 2³ = 8 (читается: «два в третьей степени равно восемь» или «третья степень числа 2 равна 8»).
В данной записи:
— a — основание степени; в выражении 2³ основанием степени является число 2.
— n — показатель степени; в выражении 2³ показателем степени является число 3.

Степень с целым показателем в случае натурального показателя означает многократное умножение основания на себя. Это самый простой и интуитивно понятный случай. Например, 5⁴ = 5 × 5 × 5 × 5 = 625.

Степень с нулевым показателем

Степень любого ненулевого числа с нулевым показателем равна 1.
Это важное правило, которое является частью общего понятия степени с целым показателем. Например: 5⁰ = 1, (−3)⁰ = 1, (2/3)⁰ = 1. Исключение составляет 0⁰ — это выражение не имеет смысла в математике.

Степень с целым отрицательным показателем

Степень с целым отрицательным показателем — это еще один важный случай. Число с отрицательным показателем степени равно дроби, у которой:
числитель — единица, а знаменатель — данное число с положительным показателем.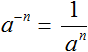
Формула степени с отрицательным показателем: a в степени -n = 1 / a в степени n

Таким образом, степень с целым показателем может быть и отрицательной, что позволяет нам работать с дробными значениями, записанными в компактной форме. Например, 2⁻³ = 1 / 2³ = 1/8.

Примеры: степень с разным показателем

Рассмотрим последовательность степеней числа 2, чтобы наглядно увидеть, как меняется степень с целым показателем в зависимости от значения показателя:

Степень с натуральным показателем в этой последовательности: 2¹, 2², 2³, 2⁴, 2⁵ (результаты: 2, 4, 8, 16, 32).
Нулевая степень в этой последовательности — это 2⁰ = 1.
Предыдущая степень с целым показателем будет уже с отрицательным показателем: 2⁻¹ = 1/2, 2⁻² = 1/4 и так далее. Вся последовательность отрицательных степеней: 2⁻⁵, 2⁻⁴, 2⁻³, 2⁻², 2⁻¹.

Вычисление степени с целым отрицательным показателем

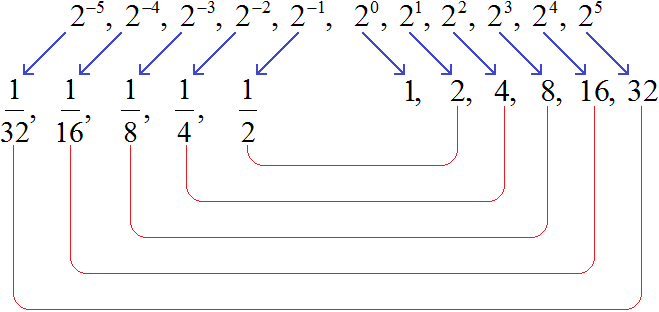
Например, возьмём число 2 и возведем его в разную степень, чтобы увидеть закономерности степени с целым показателем:

нулевая степень: 2⁰ = 1
степень с натуральным показателем:
2¹ = 2,
2² = 2 × 2 = 4,
2³ = 2 × 2 × 2 = 8 и т.д.
степень с отрицательным показателем:
2⁻¹ = 1/2,
2⁻² = 1/(2 × 2) = 1/4,
2⁻³ = 1/(2 × 2 × 2) = 1/8 и т.д.

Заметим важную закономерность: в данной последовательности значения степеней с отрицательными показателями являются обратными числами к значениям степеней с натуральными показателями. Это свойство помогает быстро вычислять степень с целым показателем любого числа.

Действия над степенями с разными показателями

Все правила действий, знакомые вам по натуральным показателям, полностью сохраняются для степени с целым показателем любого знака. Рассмотрим основные из них.

Умножение степеней с одинаковыми основаниями

При умножении степеней с одинаковыми основаниями показатели степеней складываются:

Пример: 2³ × 2⁻² = 2^{(3 + (−2))} = 2¹ = 2.

Деление степеней с одинаковыми основаниями

При делении степеней с одинаковыми основаниями из показателя степени делимого вычитается показатель делителя:

Пример: 5⁴ : 5⁻² = 5^{(4 − (−2))} = 5⁶ = 15625.

Возведение произведения в степень

Чтобы возвести произведение в степень, надо возвести в эту степень каждый сомножитель отдельно:

Пример: (2 × 3)⁻² = 2⁻² × 3⁻² = 1/4 × 1/9 = 1/36.

Возведение дроби в степень

Чтобы возвести дробь в степень, надо возвести в эту степень отдельно числитель и знаменатель:

Пример: (2/3)⁻³ = (3/2)³ = 27/8 = 3,375.

Возведение степени в степень

При возведении одной степени (положительной или отрицательной) в степень (положительную или отрицательную) показатели степеней перемножаются:

Пример: (2⁻³)² = 2^−3×2 = 2⁻⁶ = 1/64.

Поднятие степени из знаменателя в числитель и наоборот

Если в равенстве a⁻ⁿ = 1/aⁿ поменять местами левую и правую часть, то получим равенство 1/aⁿ = a⁻ⁿ. Это позволяет заменять в выражениях дробь вида 1/aⁿ на тождественно равное ей выражение a⁻ⁿ. Такое преобразование часто используется для упрощения выражений, содержащих степень с целым показателем.

Примеры решения

Рассмотрим несколько практических примеров, которые показывают, как работать с степенью с целым показателем при преобразованиях выражений.

Пример 1. Поднять степени из знаменателя дроби в числитель.
$Пример: 1/(x^2 y) = x^{-2} y^{-1}$
Решение: 1/(x² × y) = x⁻² × y⁻¹.

Пример 2. Поднять степени из знаменателя дроби в числитель.
$Пример: 2/(x^3 b^4) = 2 x^{-3} b^{-4}$
Решение: 2/(x³ × b⁴) = 2 × x⁻³ × b⁻⁴.

Пример 3. Поднять степень из знаменателя дроби в числитель.
$Пример: (3a)/b = 3a b^{-1}$
Решение: (3a)/b = 3a × b⁻¹.

Пример 4. Опустить степень из числителя дроби в знаменатель.
$Пример: a^{-5} / x^{-2} = x^2 / a^5$
Решение: a⁻⁵ / x⁻² = x² / a⁵.

Пример 5. Представить произведение 3(x + y)⁻⁴ в виде дроби, не содержащей степени с отрицательным показателем.
$Пример: 3(x+y)^{-4} = 3/(x+y)^4$
Решение: 3(x + y)⁻⁴ = 3 / (x + y)⁴.

Пример 6. Представить дробь в виде произведения.
$Пример: 3/x^2 = 3 x^{-2}$
Решение: 3 / x² = 3 × x⁻².

Почему важно понимать степень с целым показателем

Понятие степени с целым показателем лежит в основе многих разделов математики: от алгебры до математического анализа. Без него невозможно работать с многочленами, показательными функциями, решать уравнения и неравенства. Кроме того, степень с отрицательным показателем активно используется в физике (например, в формулах обратной пропорциональности), экономике и естественных науках.

Заключение

Мы подробно разобрали, что такое степень с целым показателем, и рассмотрели все три случая: натуральный, нулевой и отрицательный показатели. Вы познакомились с основными правилами действий над степенями и увидели, как они применяются на практике. Главные выводы:

Степень с целым показателем — это обобщение понятия степени для любых целых чисел.
a⁰ = 1 для любого a ≠ 0.
a⁻ⁿ = 1 / aⁿ для любого a ≠ 0.
Все правила умножения, деления и возведения в степень сохраняются для любых целых показателей.
Умение преобразовывать выражения с отрицательными показателями позволяет упрощать сложные формулы и решать более широкий круг задач.

Теперь вы уверенно можете работать с степенью с целым показателем в любых математических выражениях. Практикуйтесь на примерах, и этот раздел алгебры станет для вас простым и понятным.