В статье рассмотрим, как найти синус, косинус, тангенс, котангенс, секанс и косеканс острого угла прямоугольного треугольника. Для каждой тригонометрический функции рассмотрим: определения, рисунки, формулы, комментарии, примеры.
Синус острого угла прямоугольного треугольника
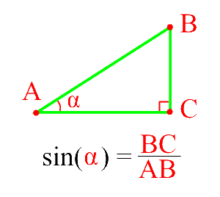
Синус острого угла прямоугольного треугольника Sin(α) — это отношение противолежащего катета(BC) к гипотенузе(AВ).
Пример:
α = 40°; BC = 4,5см; AB = 7см.
sin (40°) = 4,57 = 0,6428
Косинус острого угла прямоугольного треугольника
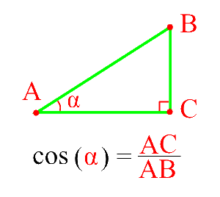
Косинус острого угла прямоугольного треугольника Cos(α) — это отношение прилежащего катета(AC) к гипотенузе(AB).
Пример:
α = 40°; AC = 6,98см; AB = 9см.
cos (40°) = 6,989 = 0,776
Тангенс острого угла прямоугольного треугольника
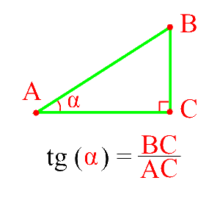Тангенсом острого угла прямоугольного треугольника Tg(α) — это отношение противолежащего катета(BC) к прилежащему катету(AC).
Пример:
α = 40°; BC = 7,552см; AC = 9см.
tg (40°) = 7,5529 = 0,8391
Тангенс можно выразить через синус и косинус:
Котангенс острого угла прямоугольного треугольника
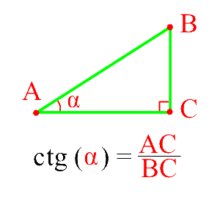Котангенс острого угла прямоугольного треугольника Ctg(α) — это отношение прилежащего катета(AC) к противолежащему катету(BC).
Пример:
α = 40°; AC = 9см; BC = 7,552см.
ctg (40°) = 97,552 = 1,1918
Котангенс можно выразить через синус и косинус: 
Сравнивая определения для тангенса и котангенса угла, можно заметить, что тангенс и котангенс угла связаны между собой соотношением: tg(α)=1/ctg(α).
Секанс острого угла прямоугольного треугольника
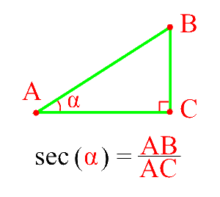Секанс острого угла прямоугольного треугольника Sec(α) — это отношение гипотенузы(AB) к прилежащему катету(AC).
Пример:
α = 40°; AB = 11,75см; AC = 9см.
Sec (40°) = 11,759 = 1,3054
Секанс можно выразить через косинус:
Косеканс острого угла прямоугольного треугольника
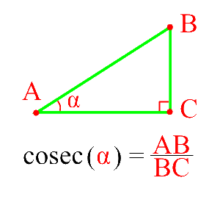Косеканс острого угла прямоугольного треугольника Cosec(α) — — это отношение гипотенузы(AB) к противолежащему катету(BC).
Пример:
α = 40°; AB = 11,75см; BC = 7,553см.
cosec (40°) = 11,757,553 = 1.5557
Косеканс можно выразить через синус: 