Формулы сокращенного умножения

Формулы сокращенного умножения включают:

• Квадрат суммы и квадрат разности двух выражений,
• Куб суммы и куб разности выражений,
• Умножение разности двух выражений на их сумму,
• Умножение разности двух выражений на неполный квадрат их суммы,
• Умножение суммы двух выражений на неполный квадрат их разности.

Квадрат суммы двух выражений

Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого выражения на второе плюс квадрат второго выражения.

Пример: преобразовать (2x + 3y)²
Выражение (2x + 3y)² это перемножение двух многочленов, каждый из которых равен (2x + 3y)
(2x + 3y)² = (2x + 3y)(2x + 3y)
Выполним умножение: (2x + 3y)² = (2x + 3y)(2x + 3y) = 4x² + 6xy + 6xy + 9y² = 4x² + 12xy + 9y²
Получим:  (2x + 3y)² = 4x² + 12xy + 9y²
То есть, мы получили выражение, которое также получается из формулы.

Геометрический смысл:
Для вычисления площади квадрата нужно возвести его сторону во вторую степень.
Площадь квадрата со стороной a будет равна a². Если увеличить сторону квадрата на b, то площадь будет равна (a + b)²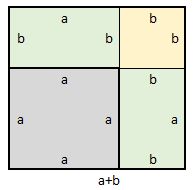

Достроим отсутствующие стороны:
Чтобы вычислить площадь этого квадрата, можно по отдельности вычислить квадраты и прямоугольники, входящие в него, затем сложить полученные результаты:
1) квадрат со стороной a — его площадь будет равна a².
2) прямоугольники со сторонами a и b — они будут равны ab.
3) квадрат со стороной b — его площадь будет равна b².

В результате получается следующая сумма площадей: a² + ab + ab + b²

Квадрат разности двух выражений

Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого выражения на второе плюс квадрат второго выражения.

Выражение (a − b)² представляет собой произведение двух многочленов, каждый из которых равен (a − b):
(a − b)² = (a − b)(a − b) = a² − ab − ab + b² = a² − 2ab + b²

Пример. Преобразовать выражение (7x − 5)²
Воспользуемся формулой квадрата разности двух выражений: (a − b)² = a² − 2ab + b²
Получим: (7x − 5)² = (7x)² − 2 × 7x × 5 + 5² = 49x² − 70x + 25
Если мы попробуем решить данный пример, не пользуясь формулой квадрата разности. У нас должен получиться тот же результат: 
(7x − 5)² = (7x − 5)(7x − 5) = 49x² − 35x − 35x + 25 = 49x² − 70x + 25.

Геометрический смысл:
Если площадь квадрата со стороной a равна a², то площадь квадрата, сторона которого уменьшена на b, будет равна (a − b)²

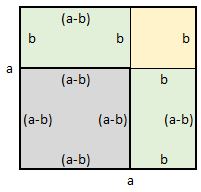Представим, что сторону квадрата, изображённого на данном рисунке уменьшили на b. У квадрата все стороны равны. Если одну сторону уменьшить на b, то остальные стороны тоже уменьшатся на b

Получился новый квадрат, который меньше предыдущего. Сторона его равна a − b, поскольку старая сторона a уменьшилась на b. Чтобы вычислить площадь этого квадрата, можно из первоначальной площади квадрата a² вычесть площади прямоугольников, которые получились в процессе уменьшения сторон старого квадрата. Покажем эти прямоугольники:
— старая площадь a² минус площадь ab минус площадь (a − b)b
a² − ab − (a − b)b
— Раскроем скобки: a² − ab − ab + b²
— Приведем подобные слагаемые: a² − 2ab + b²

Куб суммы и куб разности

Куб суммы двух выражений равен кубу первого выражения плюс утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго плюс куб второго выражения. 

Куб разности двух выражений равен кубу первого выражения минус утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго минус куб второго выражения. 

При решении задач желательно знать эти формулы наизусть. Если не запомнили  — их можно выводить самостоятельно:

Формула куба суммы двух выражений
(a + b)³ = (a + b)(a + b)² =  (a + b)(a² + 2ab + b²)
(a + b)³ = (a + b)(a² + 2ab + b²) = a³ + 2a²b + ab² + a²b + 2ab² + b³ = a³ + 3a²b + 3ab² + b³

Формула куба разности двух выражений
(a − b)³ = (a − b)(a² − 2ab + b²)
(a − b)³ = a³ − 2a²b + ab² − a²b + 2ab² − b³ = a³ − 3a²b + 3ab² − b³

Пример 1. Преобразуйте выражение (x + 1)³ в многочлен:
(x + 1)³ = x³ + 3 × x² × 1 + 3 × x × 1² + 1³ = x³ + 3x² + 3x + 1
Попробуем решить данный пример, не используя формулу куба суммы двух выражений. У нас получится тот же результат, но решение станет длиннее:
(x + 1)³ = (x + 1)(x + 1)(x + 1) = (x + 1)(x² + 2x + 1) = x³ + 2x² + x + x² + 2x + 1 = x³ + 3x² + 3x + 1

Пример 2. Преобразовать выражение (n² − 3)³ в многочлен:
(n² − 3)³ = (n²)³ − 3 × (n²)² × 3 + 3 × n² × 3² − 3³ = n⁶ − 9n⁴  + 27n² − 27

Умножение разности двух выражений на их сумму

Произведение разности двух выражений и их суммы равно разности квадратов этих выражений.

Выполним данное умножение: (a − b)(a + b) = a² + ab − ab − b² = a² − b²

Пример. Выполнить умножение (2x − 5)(2x + 5):
(2x − 5)(2x + 5) = (2x)² − 5² = 4x² − 25

При этом нет никакой разницы как располагаются сомножители (a − b) в (a + b) в формуле. Они могут быть быть записаны как (a − b)(a + b), так и (a + b)(a − b). Результат по прежнему будет равен a² − b², поскольку от перестановки множителей произведение не меняется.

Умножение разности двух выражений на неполный квадрат их суммы

Произведение разности двух выражений и неполного квадрата их суммы равно разности кубов этих выражений.

• первый многочлен (a − b) является разностью двух выражений
• второй многочлен (a² + ab + b²) является неполным квадратом суммы этих двух выражений. Неполный квадрат суммы это многочлен вида a² + ab + b². Он похож на обычный квадрат суммы a² + 2ab + b² за исключением того, что в нём произведение первого и второго выражений не удваивается.

Умножим разность (a − b) на неполный квадрат суммы a² + ab + b²
(a − b)(a² + ab + b²) = a(a² + ab + b²) − b(a² + ab + b²) = a³ + a²b + ab² − a²b − ab² − b³ = a³ − b³
То есть выражение (a − b)(a² + ab + b²) = a³ − b³

Пример. Выполнить умножение (2x − 3y)(4x² + 6xy + 9y²)
Первый многочлен (2x − 3y) это разность двух выражений 2x и 3y. 
Второй многочлен 4x² + 6xy + 9y² это неполный квадрат суммы двух выражений 2x и 3y. Это позволяет не приводя длинных вычислений, воспользоваться формулой (a − b)(a² + ab + b²) = a³ − b³. В нашем случае умножение (2x − 3y)(4x² + 6xy + 9y²) можно заменить на разность кубов 2x и 3y.
(2x − 3y)(4x² + 6xy + 9y²) = (2x)³ − (3y)³ = 8x³ − 27y³

Попробуем решить этот же пример, не пользуясь формулой (a − b)(a² + ab + b²) = a³ − b³. У нас получится тот же результат, но решение станет длиннее:
(2x − 3y)(4x² + 6xy + 9y²) = 2x(4x² + 6xy + 9y²) − 3y(4x² + 6xy + 9y²) =
8x³ + 12x²y + 18xy² − 12x²y − 18xy² − 27y³ = 8x³ − 27y³

Умножение суммы двух выражений на неполный квадрат их разности

Произведение суммы двух выражений и неполного квадрата их разности равно сумме кубов этих выражений.

• первый многочлен (a + b) является суммой двух выражений,
• второй многочлен (a² − ab + b²) является неполным квадратом разности этих двух выражений. Неполный квадрат разности это многочлен вида a² − ab + b². Он похож на обычный квадрат разности a² − 2ab + b² за исключением того, что в нём произведение первого и второго выражений не удваивается.

Умножим сумму a + b на неполный квадрат разности a² − ab + b²
(a + b)(a² − ab + b²) = a(a² − ab + b²) + b(a² − ab + b²) = a³ − a²b + ab² + a²b − ab² + b³ = a³ + b³
То есть выражение (a + b)(a² − ab + b²) равно a³ + b³

Пример. Выполнить умножение (2x + 3y)(4x² − 6xy + 9y²)
Первый многочлен (2x + 3y) это сумма двух выражений 2x и 3y.
Второй многочлен 4x² − 6xy + 9y² это неполный квадрат разности этих выражений. Это позволяет не приводя длинных вычислений, воспользоваться формулой (a + b)(a² − ab + b²) = a³ + b³. В нашем случае умножение (2x + 3y)(4x² − 6xy + 9y²) можно заменить на сумму кубов 2x и 3y
(2x + 3y)(4x² − 6xy + 9y²) = (2x)³ + (3y)³ = 8x³ + 27y³

Попробуем решить этот же пример, не пользуясь формулой (a + b)(a² − ab + b²) = a³ + b³. У нас получится тот же результат, но решение станет длиннее:
(2x + 3y)(4x² − 6xy + 9y²) = 2x(4x² − 6xy + 9y²) + 3y(4x² − 6xy + 9y²) =
8x³ − 12x²y + 18xy² + 12x²y − 18xy² + 27y³ = 8x³ + 27y³

Формулы сокращенного умножения также применяются для разложения многочлена на множители для последующих операций с многочленами:  сложения, вычитания, умножения или деления.