Таблица Брадиса: как пользоваться

Таблицы Брадиса облегчают задачу по вычислению сложных функций, поэтому ими удобно пользоваться. Они имеют одинаковую для всех функций структуру: соответствующее значение функции расположено в клетке, находящейся на пересечении столбца и строки, которые задают значение аргумента.

Таблицы Брадиса позволяют определять четыре значащих цифры любой функции. Поэтому они называются «четырехзначными». Такой точности расчетов, как правило, хватает для 90% расчетов.

Таблица Брадиса для синуса и косинуса
Таблица Брадиса для тангенса и котангенса
Таблица для секанса и косеканса

Рассмотрим как пользоваться таблицей Брадиса при расчетах на примере синусов и косинусов:

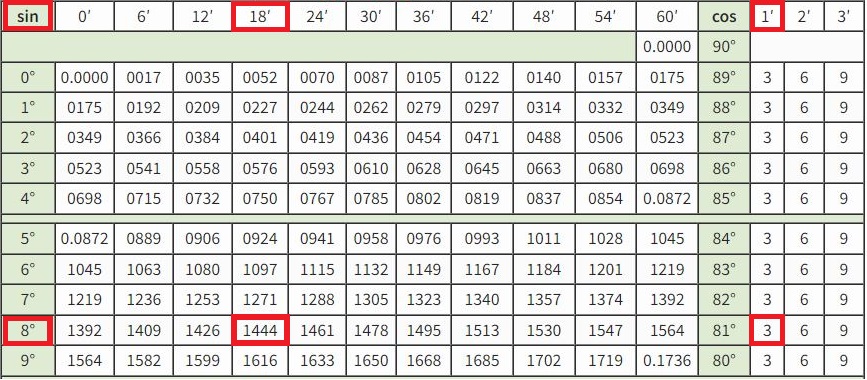
Для нахождения значений синуса: в крайнем левом столбце указаны градусы, в верхней строке указаны минуты;
Для нахождения значения косинуса: используется эта же таблица, но значения градусов находятся в четвертом столбце от края справа, а значения минут в строке снизу.
Три крайних правых столбца являются поправками для более точных вычислений.

Определить значения синуса по таблице

Допустим, следует определить, чему равно значение синуса для угла (8°18′). Для этого находим в столбце 8°, в верхней строке 18′. На их пересечении будет значение sin(8°18′)=0.1444.

Определить значения синуса, которого нет в таблице

В таблице Брадиса представлены значения углов кратных 6 минутам (0′, 6′, 12′ и т.д. до 60′). Если необходимо найти значения синуса, косинуса, тангенса или котангенса угла, который отсутствует в таблице Брадиса, следует выбирать наиболее близкое к нему значение и добавить (отнять) к нему поправку соответствующую разнице, которая может быть равна 1′, 2′, 3′.

Например, необходимо найти sin(8°19′).
Такого значения в таблице нет. Вам необходимо взять ближайшее значение из таблицы — это 8°18′ (по таблице: sin(8°18′)=0.1444).
Чтобы найти sin(8°19′) необходимо использовать поправочную таблицу справа.
sin(8°18′) и sin(8°19′) различаются на одну минуту (1′) в сторону увеличения. Значит, необходимо взять поправочное значение в 1 минуту, которое по таблице равно 3. Это означает, что к значению 0.1444 необходимо прибавить 0.0003. Получается 0.1447.
Ответ. sin(8°19′)=0.1447.

Аналогично можно получить значение для sin(8°23′). Здесь необходимо учесть, что ближайшее значение по таблице Брадиса к 23′ является 24′, т.е. нам необходимо будет уменьшить значение sin(8°24′) на поправочное значение (т.к. 23<24).
Получаем: sin(8°24′)=0.1461, тогда sin(8°23′)=0.1461-0.0003=0.1458, т.к. поправочное значение для 1′, на которое мы должны скорректировать (в данном случае уменьшить) значение, равно 3.

Другие примеры: 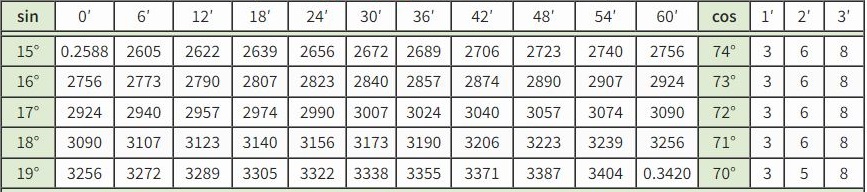sin(15°25′) = sin(15°24′) + поправка 1′ = 0.2656 + 0.0003 = 0.2659
sin(15°28′) = sin(15°30′) — поправка 2′ = 0.2672 — 0.0006 = 0.2666

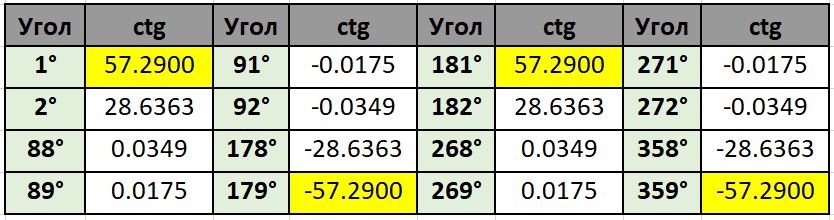
Определить значения синуса для угла больше 90°

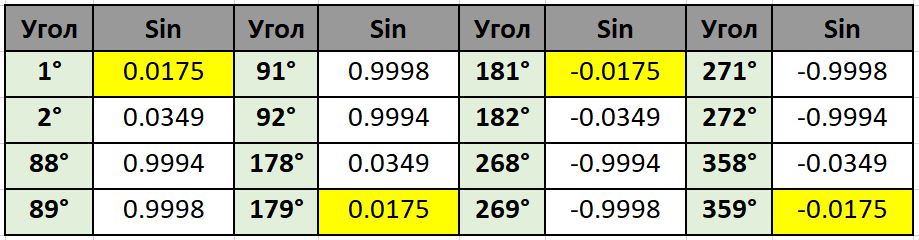
Как видно из таблицы, значения синусов повторяются для каждого промежутка: до 90°, от 91 до 180°, от 181° до 270°, от 271° до 360°. Таким образом, зная значение синуса для любого острого угла, можно найти значение для любого другого угла.

Для того, чтобы найти значение угла от 91° до 180°, нужно из 180° вычесть данный угол и найти значение синуса.
Например: sin(179°)=sin(180°-179°)=sin(1°)=0,0175.
Для того, чтобы найти значение угла от 181° до 270°, нужно из 180° вычесть данный угол и найти значение синуса, которое получится со знаком минус.
Например: sin(181°)=sin(180°-181°)=sin(-1°)=-sin(1°)=-0,0175.
Для того, чтобы найти значение угла от 271° до 360°, нужно из данного угла вычесть 360° и найти значение синуса, которое получится со знаком минус.
Например: sin(359°)=sin(359°-360°)=sin(-1°)=-sin(1°)=-0,0175.

То есть для синуса угла от 0° до 180° — значения положительные, для синуса угла от 181° до 360° — отрицательные.

Определить значения косинуса по таблице

Поскольку синус и косинус для данного угла взаимосвязаны, по таблице синусов можно определять и значения косинусов. Но аргумент для косинуса следует искать в правом столбце (четвертом справа) и в нижней строке.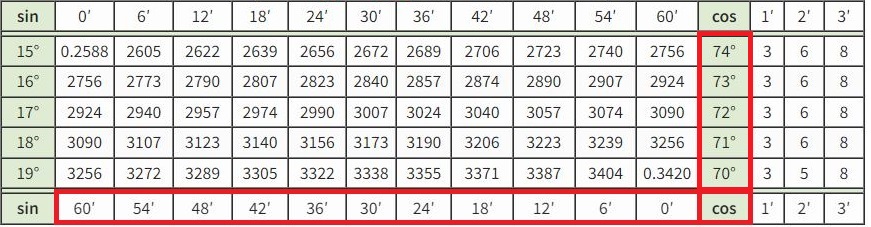

Определить значения косинуса, которого нет в таблице

При вычислении значений синуса поправка имеет положительный знак, для косинуса поправку необходимо брать с отрицательным знаком.

Примеры:
cos(15°25′) = sin(15°24′) + поправка 1′ = 0.9641 — 0.0001 = 0.9640
cos(15°28′) = sin(15°30′) — поправка 2′ = 0.9636 + 0.0002 = 0.9638

Определить значения косинуса для угла больше 90°

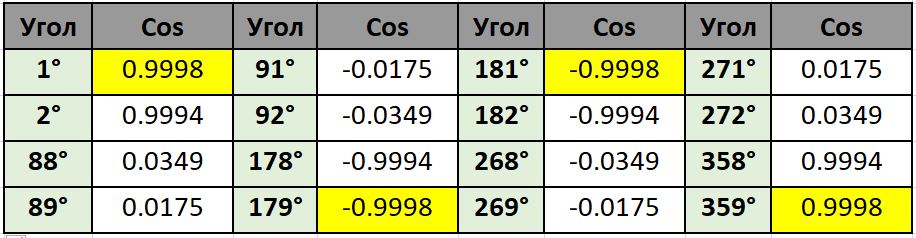
Как видно из таблицы, значения косинусов также повторяются для каждого промежутка: до 90°, от 91 до 180°, от 181° до 270°, от 271° до 360°. Таким образом, зная значение косинуса для любого острого угла, можно найти значение для любого другого угла.

То есть для косинуса угла от 0° до 90° и от 271° до 360° — значения положительные, для синуса угла от 91° до 270° — отрицательные.

Определить значения тангенса и котангенса

Таблица Брадиса для тангенса и котангенса имеет такую же структуру, поэтому ей пользоваться нужно аналогично. То есть, тангенс и котангенс для данного угла взаимосвязаны. По таблице тангенсов можно определять и значения котангенсов.

Определить значения тангенса для угла больше 90°

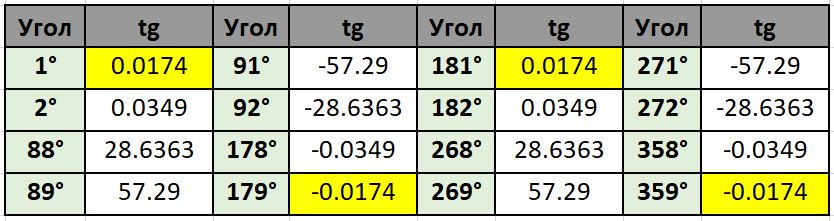
Из таблицы следует, что значения тангенса повторяются для каждого промежутка:
— до 90°, от 181° до 270° — значения положительные
— от 91 до 180°, от 271° до 360° — значения отрицательные.

Определить значения котангенса для угла больше 90°

Градусы и радианы в таблице Брадиса

Аргументы тригонометрических функций в таблицах Брадиса заданы в градусах. Для перевода градусов в радианы значение угла следует умножить на 180 и разделить на 3.1415926.

Пример для закрепления

Найти sin 40°30′ + cos 32°15′

Определение числовых данных заданного аргумента синуса и косинуса можно произвести , открыв страничку с таблицей, содержащей значения величин обеих функций одного аргумента.

Чтобы найти sin 40°30′ в крайнем левом столбце находим значение 40°, в верхней строке 30′ и находим их пересечение. Получаем 0,6494
Чтобы найти cos 32°15′ Находим пересечение 32° и 12′, т.к в таблице используются значения минут, делящиеся на 6. Получаем 0,8462. В этой же строке находим пересечение со столбцом поправки на 3′ и прибавляем к 0,8462, т.к нам необходимо найти значение 15′. Необходимо помнить, что для косинуса поправка будет иметь отрицательный знак. 0,8462+(-0,0005)=0,8457
Ответ: sin 40°30′ + cos 32°15′ = 0,6494+0,8457= 1,4951.