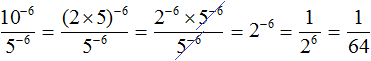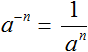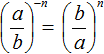Степень с целым отрицательным показателем

В статье рассмотрим степень с целым отрицательным показателем: определения, виды, вычисление степени, формулы для быстрого расчета.

Примеры степени с целым отрицательным показателем выглядят следующим образом: 2⁻², 10⁻⁷, a⁻⁸.

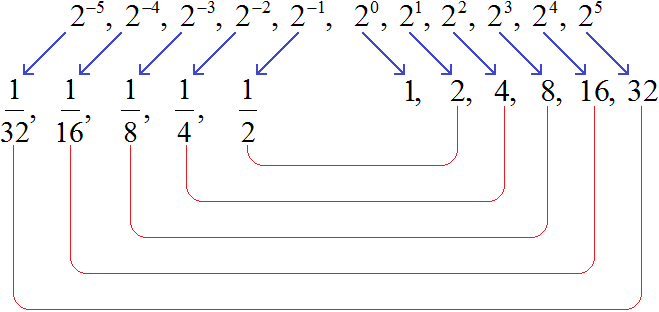
Чтобы разобраться с ними, рассмотрим следующую последовательность степеней: 2⁻⁵, 2⁻⁴, 2⁻³, 2⁻², 2⁻¹, 2⁰, 2¹, 2², 2³, 2⁴, 2⁵.

Степень с натуральным показателем в этой последовательности: 2¹, 2², 2³, 2⁴, 2⁵
Нулевая степень в этой последовательности это степень 2⁰.
Предыдущая степень с целым показателем будет уже с отрицательным показателем и выглядеть как 2⁻¹. Степень с целым отрицательным показателем в этой последовательности: 2⁻⁵, 2⁻⁴, 2⁻³, 2⁻², 2⁻¹.

Вычисление степени с целым отрицательным показателем

В отрицательную степень число возводится по-другому: если при возведении в положительную степень число увеличивается, то при возведении в отрицательную степень это число наоборот уменьшается.

Например, возьмём число 2 и возведем его в неотрицательную степень:

нулевая степень: 2⁰ =1
степень с нутуральным показателем:
2¹=2,
2²=2*2=4,
2³=2*2*2=8,
2⁴=2*2*2*2=16 и т.д.

Получили последовательность чисел, в которой каждое число больше следующего числа в 2 раза. Тогда логично предположить, что число, располагающееся до единицы, будет в два раза меньше единицы. Его можно получить, если 1 разделить на 2.

Получается, что степень 2⁻¹ =1/2.
Предыдущее число 2⁻² должно быть в два раза меньше, чем 2⁻¹. Чтобы его получить разделим на 2 и получим 2⁻² =1/(2*2)=1/4.
Предыдущее число 2⁻³ должно быть в два раза меньше, чем 2⁻². Чтобы его получить разделим на 2 и получим 2⁻³ =1/(2-2*2)=1/8.

Заметим, что в данной последовательности значения степеней с отрицательными показателями являются обратными числами к значениям степеней с натуральными показателями:

Значение степени в 2² есть число 4, а значение степени 2⁻² есть число 1/4. Числа 4 и 1/4 являются обратными друг другу.
Значение степени в 2³ есть число 8, а значение степени 2⁻³ есть число 1/8. Числа 8 и 1/8 являются обратными друг другу.

Можно сделать вывод, что для вычисления степени с отрицательным показателем, нужно записать дробь, в числителе которой единица, а в знаменателе та же самая степень, но с противоположным показателем.

Таким образом, чтобы вычислить степень вида 2⁻ⁿ , можно воспользоваться следующим правилом:

Правило работает только тогда, когда a ≠ 0. Если a будет равным нулю, то в знаменателе получим 0, а на нуль делить нельзя.

Данное правило можно доказать, используя правило деления степеней с одинаковыми основаниями. Допустим, нам нужно высислить степень в целым отрицательным показателем 2⁻². Использую правило деления степеней с одинаковыми основаниями записшем 2⁻² как 2^(3-5) = 2³: 2⁵. Запишем это деление в виде дроби. Получим:

Пример 1. Найти значение выражения 3⁻³

Пример 2. Найти значение выражения (-2/3)⁻³

Формула для возведения обыкновенных дробей в отрицательную степень:

Желательно уметь возводить обыкновенную дробь в отрицательную степень как с помощью формулы, так и без неё.

Тождественные преобразования степеней с целым отрицательным показателем

Все тождественные преобразования, которые мы рассматривали при изучении степени с натуральным показателем, сохраняются и для степеней с целыми отрицательными показателями.

Пример 3. Найти значение выражения 2⁻¹× 2⁻³.
Воспользуеся основным свойством степени:
2⁻¹ × 2⁻³ = 2^{−1 + (−3)} = 2⁻⁴=1/16

Пример 4. Найти значение выражения 5⁻¹⁵× 5¹⁶.
Воспользуемся основным свойством степени:
5⁻¹⁵× 5¹⁶= 5^{−15 + 16}= 5¹= 5

Пример 5. Найти значение выражения (10⁻⁴)⁻¹Воспользуемся правилом возведения степени в степень:
(10⁻⁴)⁻¹ = 10^{−4 × (−1)} = 10⁴ = 10000

Пример 6. Найти значение выражения (10⁻⁶)/(5⁻⁶)
Представим число основание 10 в виде произведения 2×5. Тогда числитель примет вид (2×5)⁻⁶