Рациональные числа

Рациональные числа — это все числа (положительные и отрицательные), которые могут быть представлены в виде обыкновенной дроби, также число 0 (ноль).
То есть, если число можно получить делением двух целых чисел — это число рациональное.

К рациональным числам относятся:

натуральные числа — числа, начиная с 1, получаемые при счете предметов: 1, 2, 3, 4, 5 и т.д.
целые числа — это множество чисел, которое включает натуральные числа, противоположные натуральным отрицательные числа и ноль. Примеры: -170; -6; 0; 23; 1055.
обыкновенные дроби — это числа вида a/b, где a – числитель, b — знаменатель. Примеры: 1/3, 1/15.
конечные десятичные дроби -это дроби или смешанные числа, имеющее знаменатель 10, 100, 1000, 10000 и т. д. Примеры: 0,25; 23,123; 8/10; 9/1000 и др.
бесконечные периодические дроби — это дроби, у которых одна цифра или группа цифр повторяются. Повторяющаяся группа цифр называется периодом и записывается в скобках. Примеры: 0,(6); 0,(3); 0,6(81).

Множество рациональных чисел принято обозначать латинской буквой Q.

Отличие между целыми, натуральными и рациональными числами

Натуральные числа — это числа, которые мы используем при счете: 1,2,3,4,5…100… и т.д. Наименьшее натуральное число — 1, Наибольшего натурального числа не существует. Они используются для подсчета чего-то конкретного: два кота, пять лошадей, двадцать стульев и т.д.

Целые числа — это натуральные числа + противоположные им числа + ноль.
Если два числа отличаются друг от друга знаком — их называют противоположными.
Например: +2 и -2, +7 и -7. Знак «плюс» обычно не пишут, и если перед числом нет никакого знака, значит оно положительное. Числа, перед которыми стоит знак «минус», называют отрицательными.

Рациональные числа — включают целые числа + дроби (обыкновенные, десятичные, периодические).
Любое рациональное число может быть представлено в виде дроби, у которой:
➜ числитель — целое число,
➜ знаменатель — натуральное число.

Но не все числа можно назвать рациональными. Примеры чисел, которые не относятся к рациональным числам:
— бесконечные непериодические дроби,
— корни чисел, результатом которых будет бесконечная непериодическая дробь (√3),
— ? (число пи).

Обратные числа

Обратное число — это число, на которое надо умножить данное число, чтобы получить единицу.
Например: числа 5 и 1/5 будут взаимно обратными, так как их произведение будет равно единице.
Так как на ноль делить нельзя, то число ноль не имеет обратного числа.

Противоположные рациональные числа

Противоположные числа — это два числа, которые отличаются друг от друга знаками.
Любое рациональное число имеет свое противоположное число.
Число и противоположное число располагаются на координатной прямой симметрично относительно начала координат. Другими словами, оба этих числа равноудалены от начала координат.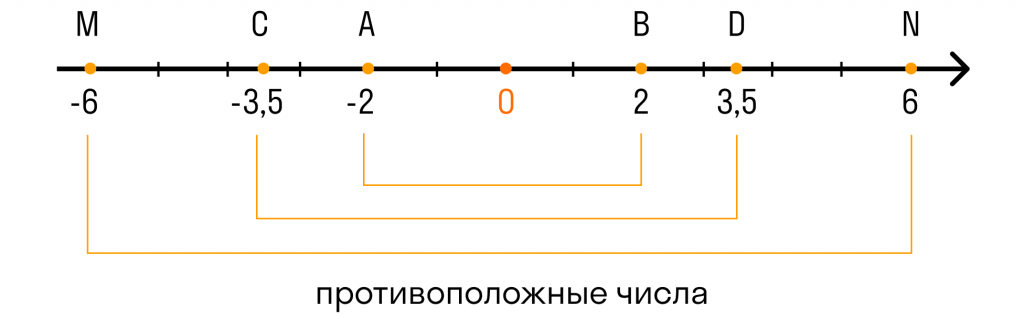

Модуль числа

Модуль числа — это расстояние от начала координат до точки координатной прямой, соответствующей этому числу. Обозначение: |а|.
Если мы возьмем некоторое число «а» и отметим его на координатной прямой точкой A, то модуль числа «а» — это расстояние от начала координат (ноль) до точки A.

модуль положительного числа — само число,
модулем отрицательного числа — противоположное ему число,
модуль ноля — ноль.

Свойства сложения и умножения рациональных чисел

Пусть а, b и c — любые рациональные числа.

Основные свойства сложения рациональных чисел

Переместительное свойство сложения: a + b = b + a.
Сочетательное свойство сложения: (a + b) +c = a + (b + c).
Сложение рационального числа и нуля не изменяет это число: a + 0 = a.
Сумма противоположных чисел всегда равна нулю: a + (-a) = 0.

Основные свойства умножения рациональных чисел

Переместительное свойство умножения: ab = ba.
Сочетательное свойство умножения: (a * b) * c = a * (b * c).
Произведение рационального числа и единицы не изменяет это число: a * 1 = a.
Произведение произвольного рационального числа на ноль равно нулю: a * 0 = 0 или 0 * a = 0.
Произведение обратных чисел равно единице: a * a−1 = 1 (у нуля нет обратного числа).

Другие свойства рациональных чисел

Распределительное свойство умножения относительно сложения: a * (b + c) = a * b + a * c.
Умножение рациональных чисел с разными знаками: (-a) * b = -ab.
запомнить: «плюс на минус — это минус, минус на плюс — это минус».
Умножение отрицательных рациональных чисел: (−a) * (−b) = ab.
запомнить: «минус на минус — это плюс».

Свойства вычитания и деления рациональных чисел.

Свойства вычитания и деления можно записать, как обратные к сложению и умножению:

Разность (a — b) можно записать, как сумму a + (-b),
Частное a/b равно произведению a * 1/b−1, при b ≠ 0.

Все рациональные числа подчиняются общим законам математики.

Сравнение рациональных чисел

Из двух положительных чисел больше то число, модуль которого больше.
Пример: 10 > 3
Из двух отрицательных чисел больше то число, модуль которого меньше.
Пример: -10 < -3

Если сравнивать отрицательное и положительное числа, то любое отрицательное число будет меньше любого положительного числа. Например, −10 < 3 или 10 > -3.

Сложение и вычитание рациональных чисел

Чтобы сложить рациональные числа с разными знаками, нужно из большего модуля вычесть меньший модуль, и перед полученным ответом поставить знак того рационального числа, модуль которого больше.
Пример: (+10) + (-30)
1. Модуль числа (-30) больше, чем модуль числа 10, поэтому мы из 30 вычитаем 10: 30-10 = 20
2. Ставим знак того рационального числа, модуль которого больше (знак «-«) и получаем: -20.
Пример: (−3,2) + (+4,3) = |+4,3| − |−3,2| = 1,1
1. Модуль числа 4,3 больше, чем модуль числа −3,2 поэтому мы из 4,3 вычитаем 3,2: 4,3-3,2 = 1,1
2. Ответ положителен, поскольку перед ответом должен стоять знак того рационального числа, модуль которого больше. А модуль числа 4,3 больше, чем модуль числа −3,2

Чтобы сложить отрицательные рациональные числа, нужно сложить их модули и перед полученным ответом поставить минус.
Пример: (-10) + (-30)
1. Складываем модули чисел: 30+10 =40
2. Перед полученным ответом ставим минус и получаем -40.

Примечание. Заключать в скобки каждое рациональное число вовсе необязательно. Делается это для удобства, чтобы хорошо видеть какие знаки имеют рациональные числа.
Сложение и вычитание рациональных чисел подчиняются общим законам математики.

Умножение рациональных чисел

Чтобы перемножить рациональные числа с разными знаками, нужно перемножить их модули и перед полученным ответом поставить минус.
Пример: (+5)×(-3)
1. Модуль числа (+5) равен 5, а модуль числа (-3) равен 3. Поэтому находим произведение 5×3=15
2. Перед ответом ставим минус, получаем (-15).

Чтобы перемножить отрицательные рациональные числа, нужно перемножить их модули и перед полученным ответом поставить плюс.
Пример: (-6)×(-2)
1. Модуль числа (-6) равен 6, а модуль числа (-2) равен 2. Поэтому находим произведение 6×2=12
2. Перед ответом ставим плюс, получаем (+12) или 12.

Умножение рациональных чисел также подчиняются общим законам математики.