Одночлены: определение и действия с ними

Одночлены — это любое число, переменная, любая степень, а также произведение чисел, переменных и степеней, с которыми можно совершать разные математические действия. Примеры одночленов: 9, 5², x, 5a; 3ab² ;  −6²aa²b³. 

Приведение одночлена к стандартному виду

Приведение одночлена к стандартному виду заключается в умножении однотипных множителей, входящих в этот одночлен. То есть числа нужно перемножать с числами, переменные с переменными, степени со степенями. В результате этих действий получается упрощённый одночлен, который тождественно равен предыдущему. Важно: в одночлене степени можно перемножать только в том случае, если они имеют одинаковые основания.

Рассмотрим следующий одночлен:  3a²5a³b²
 — числа 3 и 5 перемножим и получим число 15,
— степени a² и a³ имеют одинаковое основание a,  поэтому мы можем записать результат a⁵,
— степень b² остаётся без изменений.
Получили результат: 3a²5a³b² = 15a⁵b²

Для того, чтобы далее рассматривать одночлены и действия с ними, вспомним тему «Степень с натуральным показателем«

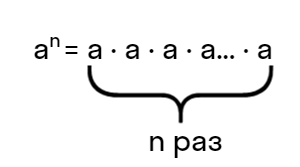
где: a — основание степени; n — показатель степени.

Коэффициент одночлена

• Числовой сомножитель (в примере 15) называют коэффициентом одночлена. Приводя одночлен к стандартному виду, коэффициент нужно записывать в первую очередь, и только потом переменные и степени.
• Если коэффициент в одночлене отсутствует, то говорят, что коэффициент равен единице.
  Например, для одночлена ab коэффициентом является 1, поскольку ab это произведение единицы и ab: abc = 1×ab.
• Если перед одночленом стоит знак минуса, то коэффициент равен минус единице. Например, для одночлена —ab коэффициентом является -1, поскольку ab это произведение -1 и ab.

Степень одночлена

Степенью одночлена называют сумму показателей степеней всех переменных входящих в этот одночлен.  Показатель числового множителя при этом не считается.
Если одночлен не содержит переменных или степеней, а состоит из числа, то говорят, что степень такого одночлена равна нулю.  

Примеры:

• Степенью одночлена 15a⁵b² является 7: переменная a имеет степень 5, а переменная b — 2. Отсюда 5 + 2 = 7. Показатель числового сомножителя 15 считать не нужно, поскольку нас интересуют только показатели переменных.
• Степенью одночлена 7ab² является 3:  переменная a имеет показатель 1, а переменная b — 2. 
• Степень одночлена 11 равна нулю, так как это число.

Не следует путать степень одночлена и степень числа:

• Степень числа это произведение из нескольких одинаковых множителей.
• Степень одночлена это сумма показателей всех переменных входящих в этот одночлен.

Сложение и вычитание одночленов

Чтобы сложить (вычесть) одночлены, нужно сложить (вычесть) их коэффициенты, а буквенную часть оставить без изменений.

Чтобы складывать и вычитать одночлены, они должны иметь одинаковую буквенную часть. Коэффициенты могут быть любыми. Сложение и вычитание одночленов это по сути представляет собой приведение подобных слагаемых.

Пример 1. Сложить одночлены 6a²b и 2a²b:
сложим коэффициенты 6 и 2, а буквенную часть 6a²b оставим без изменений.
Получим: 6a²b + 2a²b = 8a²b

Пример 2. Вычесть из одночлена 5a²b³ одночлен 2a²b³
Решение: 5a²b³ − 2a²b³ = 5a²b³ −2a²b³ = 3a²b³

Умножение одночленов

Чтобы перемножить одночлены, нужно перемножить их числовые и буквенные части.

Пример 3. Перемножить одночлены 5x и 8y
Перемножим числовые и буквенные части по отдельности: 5x × 8y = (5 × 8) × (x × y) = 40xy

Пример 4. Перемножить одночлены 5x²y³ и 7x³y²c
Перемножим числовые и буквенные части по отдельности. В процессе умножения будем применять правило перемножения степеней с одинаковыми основаниями. Перемножаемые сомножители будем заключать в скобки:
5x²y³ × 7x³y²c = (5 × 7) × (x²x³) × (y³y²) × c = 35x⁵y⁵c

Пример 5. Перемножить одночлены −5a²bc и 2a²b⁴
−5a²bc × 2a²b⁴ = (−5 × 2) × (a²a²) × (bb⁴) × c = −10a⁴b⁵c

Деление одночленов

Для того, чтобы разделит один многочлен на другой, нужно коэффициент первого одночлена разделить на коэффициент второго одночлена, а буквенную часть первого одночлена разделить на буквенную часть второго одночлена. При этом используется правило деления степеней.

Пример 6. Разделить одночлен 8a²b² на одночлен 4ab. 
Разделим коэффициент делимого на коэффициент делителя, получим 8 : 4 = 2.
Теперь делим буквенную часть:
— в делимом содержится a², в делителе — просто a. Делим a² на a, получаем a, поскольку a² : a = a^2 − 1 = a. 
— в делимом содержится b², в делителе — просто b. Делим b² на b, получаем b, поскольку b² : b = b^2 − 1 = b. Значит, при делении одночлена 8a²b² на одночлен 4ab получается одночлен 2ab.

Если переменная есть только в одном многочлене:

Если в делителе окажется переменная, которой нет в делимом, то  деление невозможно.

Например, одночлен 6xy² нельзя разделить на одночлен 3xyz, так как в делителе 3xyz содержится переменная z, которая не содержится в делимом 6xy².

Но в некоторых дробях, если невозможно выполнить деление, бывает возможным выполнить сокращение. Делается это с целью упростить выражение.

*сокращение дроби это деление числителя и знаменателя на одно и то же число.
Так, в примере нельзя разделить одночлен 6xy² на одночлен 3xyz. Но можно сократить эту дробь на одночлен 3xy.

Если в делимом содержится переменная, которая не содержится в делителе, то деление будет возможным. В этом случае переменная, которая отсутствовала в делителе, будет перенесена в частное без изменений.

Например, при делении одночлена 4x²y²z на 2xy, получается 2xyz. 

Если одна из степеней, входящая в делимое, имеет показатель меньший, чем показатель той же степени из делителя, то деление одночлена на одночлен также невозможно.

Например, разделить одночлен 2x на одночлен x² нельзя, поскольку степень x, входящая в делимое, имеет показатель 1, тогда как степень x², входящая в делитель, имеет показатель 2. Мы не сможем найти частное, которое при перемножении с делителем x² даст в результате делимое 2x.

Возведение одночлена в степень

При возведении степень одночлена каждый из множителей возводится в степень. Затем полученные результаты перемножаются: (a × b)ⁿ = aⁿ × bⁿ 

Пример 7. Возвести одночлен xy во вторую степень.
Чтобы возвести одночлен xy во вторую степень, нужно возвести во вторую степень каждый множитель этого одночлена: (xy)² = x²y²

Пример 8. Возвести одночлен −a²bc³ в пятую степень.
В данном примере коэффициентом одночлена является −1. Этот коэффициент тоже нужно возвести в пятую степень: 
(−a²bc³)⁵ = (−1)⁵ × (a²)⁵ × b⁵ × (c³)⁵ = −1a¹⁰b⁵c¹⁵ = −a¹⁰b⁵c¹⁵
Когда коэффициент равен −1, то саму единицу не записывают. Записывают только минус и потом остальные множители одночлена.

Пример 9. Представить одночлен 121a⁶ в виде одночлена, возведённого в квадрат.
— число 121 получается, если число 11 возвести в квадрат — это первый множитель.
— степень a⁶ получается, если возвести в квадрат степень a³ — это второй множитель.
Таким образом, если произведение 11a³ возвести во вторую степень, то получится  121a⁶
(11a³)² = 11² × (a³)² = 121a⁶

Разложение одночлена на множители

Поскольку одночлен является произведением чисел, переменных и степеней, то он может быть разложен на множители, из которых состоит.

Пример 10. Разложить одночлен 3a³b² на множители
Данный одночлен можно разложить на множители:
3a³b² = 3×a×a×a× b×b =  3×a×a×a×b² = 3×a³×b×b