МНОГОГРАННИКИ (объемные геометрические фигуры): определения, формулы

Многогранники (объемные геометрические фигуры) : определения, формулы периметра поверхности и площади. Виды: призма, параллелепипед ( в т.ч. прямоугольный параллелепипед , куб), пирамида ( в т.ч. усеченная пирамида).

Призма

Призма — многогранник, у которого две грани — равные многоугольники (основания), лежащие в параллельных плоскостях, а остальные грани (боковые) — параллелограммы, имеющие общие стороны с этими многоугольниками.
Многоугольник, лежащий в основании, определяет название призмы: треугольник — треугольная призма, четырёхугольник — четырёхугольная призма; пятиугольник — пятиугольная призма (пентапризма) и т. д.
Прямая призма – призма, у которой боковые ребра перпендикулярны к плоскости основания (если нет – наклонная).
Правильна призма – призма, в основании которой лежит правильный многоугольник.
Высота призмы – перпендикуляр, опущенный из любой точки одного основания. на плоскость другого.

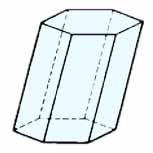Формулы для призмы:

Объем призмы: V = S_o∙h
Площадь поверхности: S = 2∙S_o + S_бокГде: V — объем призмы, S_o — площадь основания, h – высота, S_бок — площади всех боковых граней.

Параллелепипед

Параллелепипед — это призма, основание которой — параллелограмм.

Свойства параллелепипеда:

Параллелепипед имеет шесть граней и все они параллелограммы.
Противоположные грани попарно равны и параллельны.
Параллелепипед имеет четыре диагонали.
Все диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам.
Основанием параллелепипеда может быть любая грань.

Типы параллелепипеда

Прямой параллелепипед — это параллелепипед, у которого 4 боковые грани прямоугольники.
Прямоугольный параллелепипед — это параллелепипед, у которого все грани — прямоугольники.
Наклонный параллелепипед — это параллелепипед, боковые грани которого не перпендикулярны основаниям.
Ромбоэдр — параллелепипед, грани которого являются равными ромбами.

Куб — параллелепипед, грани которого являются квадратами. Все грани куба равны.

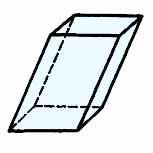Формулы для параллелепипеда:

Объем параллелепипеда: V = S_o∙h
Площадь поверхности: S = 2∙S_o + S_бокГде: V — объем параллелепипеда, S_o — площадь основания, h – высота, S_бок — площади всех боковых граней.

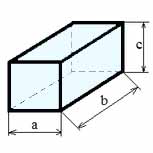Формулы для прямоугольного параллелепипеда:

Объем прямоугольного параллелепипеда: V = a∙b∙c = S_o∙ c
Площадь поверхности прямоугольного параллелепипеда:
S = 2·(S_a+S_b+S_c) или S= 2· (a·b+ b·c+ a·c)
Диагональ: d =√(a²+b²+c²)
Где: V — объем прямоугольного параллелепипеда, a — длина, b — ширина, с – высота, So — площадь основания, S_a,S_b_,S_c — площади соответствующих сторон.

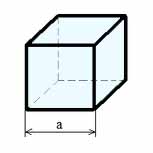Формулы для куба:

Объем куба: V = a³Площадь поверхности куба: S = 6·a²Диагональ: d = a√3
Где: V — объем куба, a — длина грани куба.

Пирамида

Пирамида — многогранник, одна из граней которого (основание) — произвольный многоугольник, а остальные грани (боковые) — треугольники, имеющие общую вершину.
По числу углов основания различают пирамиды треугольные (тетраэдр), четырёхугольные и т. д.
Вершина пирамиды – общая точка для всех треугольников.
Высота пирамиды – перпендикуляр, опущенный из вершины пирамиды на ее основание.
Правильная пирамида – пирамида, у которой основание — правильный многоугольник, высота опускается в центр основания. В правильной пирамиде все боковые ребра равны, все боковые грани — равнобедренные треугольники. Высота треугольника боковой грани правильной пирамиды называется — апофема правильной пирамиды.

Правильная треугольная пирамида — это многогранник, у которого одна грань — основание пирамиды — правильный треугольник, а остальные — боковые грани — равные треугольники с общей вершиной. Высота опускается в центр основания из вершины.
Правильный тетраэдр – это тетраэдр, у которого все грани — равносторонние треугольники.
Правильная четырехугольная пирамида — это многогранник, у которого одна грань — основание пирамиды — квадрат, а остальные — боковые грани — равные треугольники с общей вершиной. Высота опускается в центр пересечения диагоналей квадрата основания из вершины.

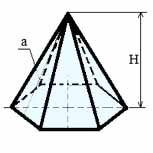Формулы для правильной пирамиды:

Объем правильной пирамиды: V = 1/3 · (S_o · h)
Площадь боковой поверхности правильной пирамиды: S_бок = ½ · P_о· a
Где: V — объем пирамиды, S_o — площадь основания пирамиды, S_бок — площадь боковой поверхности, P_о — периметр основания правильной пирамиды, h — высота пирамиды. a — апофема правильной пирамиды.

Формулы для правильной треугольной пирамиды:

Объем правильной треугольной пирамиды: V = h·a² / (4/√3)
Где: a — сторона правильного треугольника — основания правильной треугольной пирамиды, h — высота правильной треугольной пирамиды

Формулы для правильной четырехугольной пирамиды:

Объем правильной четырехугольной пирамиды: V = 1/3 · h · a²Где: a — сторона квадрата — основания правильной четырехугольной пирамиды, h — высота правильной четырехугольной пирамиды.

Формулы для тетраэдра:

Объем тетраэдра: V = (√2 / 12) · a³Где: V — объем тетраэдра, a — длина ребра тетраэдра.

Усеченная пирамида

Усеченная пирамида — часть пирамиды между ее основанием и сечением (сечение параллельно основанию пирамиды и делит ее на две части).
Основание пирамиды и сечение — два основания усеченной пирамиды.
Высота усеченной пирамиды — расстояние между основаниями усеченной пирамиды.
Правильная усеченная пирамида — пирамида, которая получена из правильной пирамиды. Все боковые грани правильной усеченной пирамиды — это равные равнобокие трапеции. Высота трапеции боковой грани правильной усеченной пирамиды называется — апофема правильной усеченной пирамиды.

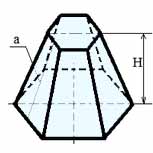Формулы для усеченной пирамиды:

Объем усеченной пирамиды равен разности двух полных пирамид.
Объем правильной усеченной пирамиды:
V = 1/3 · h · (S_осн1 + S_осн2 + √(S_осн1S_осн2))
Боковая поверхность правильной усеченной пирамиды:
S_бок = ½ (P_осн1 + P_осн2) · a
Где: S_осн1, S_осн2 — площади верхнего и нижнего основания усеченной пирамиды, h — высота усеченной пирамиды, P_осн1, P_осн2 — периметры верхнего и нижнего оснований правильной усеченной пирамиды, a — апофема правильной усеченной пирамиды.

Также на сайте описаны тела вращения, в том числе :определения и формулы.