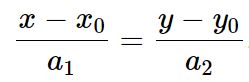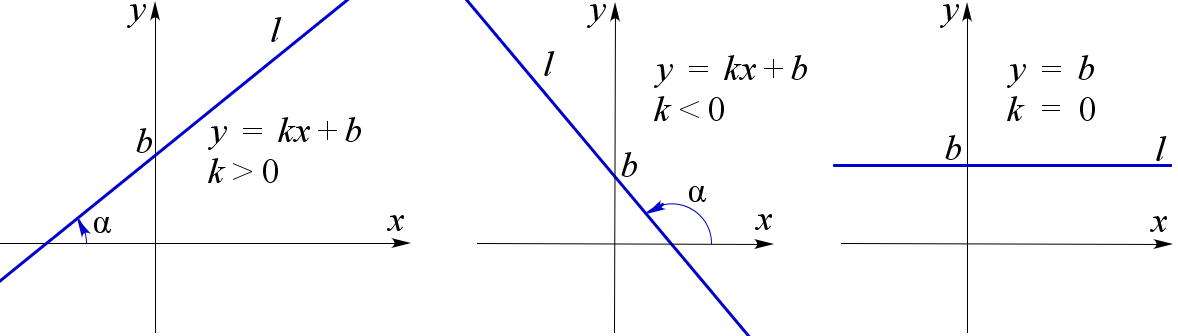В статье: 1) Общее уравнение прямой на плоскости координат,
2) Уравнение прямой, проходящей через данную точку перпендикулярно данному вектору,
3) уравнение прямой, проходящей через данную точку с заданным направляющим вектором,
4) Уравнение прямой с угловым коэффициентом.
Общее уравнение прямой на плоскости координат
Общее уравнение прямой в системе координат на плоскости — это уравнение вида Ax+By+C=0, где A≠0 или B≠0. Любое уравнение такого вида задаёт прямую.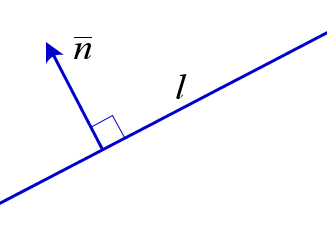
Общее уравнение прямой на плоскости, проходящей через данную точку перпендикулярно данному вектору
В прямоугольной декартовой системе координат общее уравнение прямой l, проходящей через точку M0(x0,y0) перпендикулярно ненулевому вектору n имеет вид: A(x−x0)+B(y−y0)=0.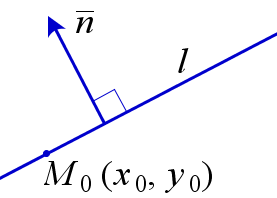
Уравнение прямой на плоскости, проходящей через данную точку с заданным направляющим вектором
В декартовой системе координат уравнение прямой l, проходящей через точку M0(x0,y0) параллельно ненулевому вектору a имеет вид:
- Каноническое уравнение
Уравнение имеет вид:
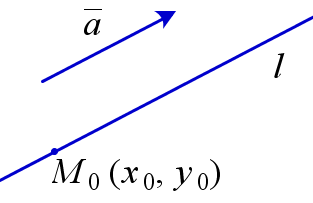
Ненулевой вектор, параллельный данной прямой или лежащий на ней, называется направляющим вектором этой прямой.
Точка M(x,y) лежит на прямой l тогда и только тогда, когда её координаты удовлетворяют данной системе при некотором t∈R.
Уравнение прямой с угловым коэффициентом
Уравнение вида y=kx+b задаёт в прямоугольной декартовой системе координат прямую l, не параллельную оси ординат.
Число k называется угловым коэффициентом прямой l. Угловой коэффициент прямой равен тангенсу угла наклона прямой l к положительному направлению оси абсцисс: k=tgα.
Угол наклона отсчитывают от этой оси до прямой l против часовой стрелки. Если прямая l параллельна оси абсцисс или совпадает с нею, то угол наклона считается нулевым.
Коэффициент b равен ординате точки пересечения прямой l с осью ординат.