В статье рассмотрим степень с дробным показателем:
Какими свойствами обладает степень с дробным показателем (дробная степень)?
Как выполнить возведение числа в дробную степень?
Степенью числа a (где a>0) с рациональным показателем, который равен (n/m) называется число вида: 
, где где m — целое число, n — натуральное число (n>1).
Таким образом, число с дробным показателем степени равно корню с показателем, равным знаменателю, и подкоренным числом в степени, равной числителю.
При этом a<0 степень с дробным показателем не определяется. 
Чтобы извлечь корень из степени, надо показатель степени разделить на показатель корня. 
Следовательно, если показатель степени не делится на показатель корня, то получается дробная степень. 
Свойства степеней с дробным показателем
Все свойства степеней из курса алгебры 7 класса выполняются и для степеней с дробными показателями.
Для упрощения вычислений при возведении числа в дробную степень удобно использовать следующее свойство корня: 
Чтобы было легче решать вычислять степени с дробным показателем:
- Если показатель степени — десятичная дробь, нужно предварительно перевести ее в обыкновенную.
- Смешанное число нужно предварительно перевести в неправильную дробь.
- При возведении обыкновенной дроби в степень с отрицательным показателем удобно использовать формулу (только для a>0):
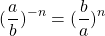
Поэтому для степеней с дробным показателем также используем эту формулу: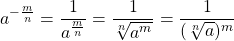
Следует обратить внимание, что основание не может быть отрицательным числом, а показатель степени может быть как положительным, так и отрицательным.
Действия над степенями с дробными показателями
Действия над степенями с дробными показателями совершаются по тем же правилам, которые установлены для степеней с целым показателем.
При умножении дробных степеней с одинаковыми основаниями их показатели складываются:
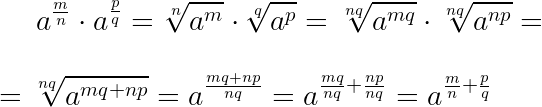
При делении дробных степеней с одинаковыми основаниями из показателя делимого вычитается показатель делителя:
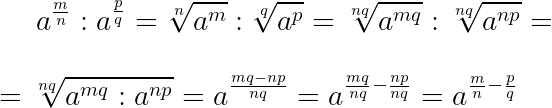
Чтобы возвести степень в другую степень, в случае дробных показателей, достаточно перемножить показатели степеней:
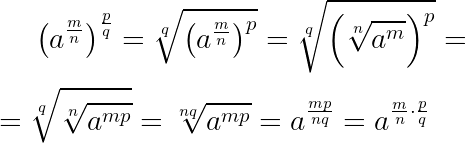
Чтобы извлечь корень из дробной степени, достаточно показатель степени разделить на показатель корня: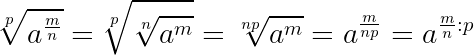 
Правила действий применимы не только к положительным дробным показателям, но и к отрицательным.