Сложение и вычитание логарифмов с разными основаниями

Для того, чтобы выполнить сложение или вычитание логарифмов с разными основаниями, нужно:

1. Привести их к одному основанию, используя формулу приведения.
2. Выполнить сложение или вычитание логарифмов с одинаковыми основаниями.

Преобразования стандартные, но необходимо знать основные свойства логарифмов.

Пример: 4*log₁₆(5) + log₂(3) .
Для этого один из логарифмов переведем к другому основанию.
Например,  log₁₆(5) приведем к основанию 2.

1. Переход к другому основанию

Формула перехода к новому основанию позволяет сделать преобразования для дальнейших вычислений.

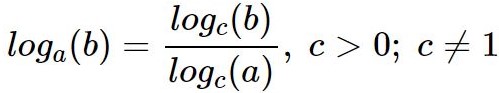
Пример: log₁₆(5) = log₂(5) / log₂(16) 
log₂(16) = 4, поэтому  log₁₆(5) = log₂(5) / 4

Частный случай формулы перехода к новому основанию

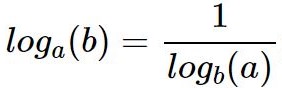
Пример: log₁₆(5) = 1/log₅(16) 

Для других преобразований логарифмов используйте их основные свойства.

2. Сложение и вычитание логарифмов с одинаковыми основаниями после приведения

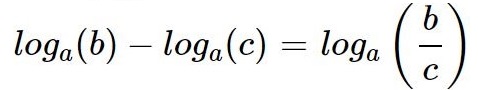
Сумма логарифмов равна логарифму произведения,
Разность логарифмов равна логарифму частного.
Это верно если: числа а, х, у — положительные; а ≠ 1.

Получаем:
— из формулы приведения: log₁₆(5) = log₂(5) / 4
— подставляем в пример: 4*log₁₆(5) + log₂(3)  = 4 * log₂(5) / 4 + log₂(3)  = log₂(5) + log₂(3) 
— складываем по формуле: log₂(5) + log₂(3) = log₂(5*3) log₂(15) 

Онлайн калькуляторы для вычисления логарифмов

Калькулятор логарифмов онлайн (для всех типов логарифмов)
Калькулятор десятичного логарифма
Калькулятор натурального логарифма

Также по теме:

Понятие логарифма
Основные свойства логарифмов
Сложение и вычитание логарифмов с одинаковыми основаниями