Признаки равенства треугольников

Два треугольника называются равными, если все их соответствующие стороны и все соответствующие углы равны.

Существуют следующие основные признаки равенства треугольников:

По двум сторонам и углу между ними,
По стороне и двум прилежащим к ней углам
По трем сторонам.

Первый признак равенства треугольников

Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то данные треугольники равны.
На рисунке: AB=A1B1, AC=A1C1, ∠BAC=∠B1A1C1 ⇒ △ABC=△A1B1C1.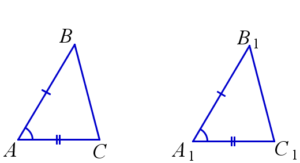

Второй признак равенства треугольников

Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то данные треугольники равны.
На рисунке: AC=A1C1, ∠BAC=∠B1A1C1, ∠BCA=∠B1C1A1 ⇒ △ABC=△A1B1C1.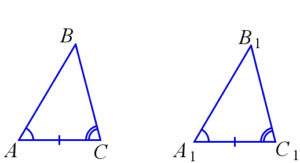

Третий признак равенства треугольников

Если три стороны одного треугольника соответственно равны трём сторонам другого треугольника, то данные треугольники равны.
На рисунке: AB=A1B1, AC=A1C1, BC=B1C1 ⇒ △ABC=△A1B1C1.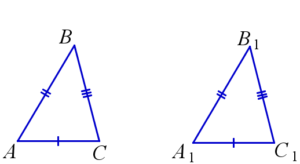

Другие признаки равенства треугольников

Три признака равенства треугольников — основные. Но есть и другие признаки, которые стоит запомнить.

1. Если угол, сторона, противолежащая этому углу, и высота, опущенная на другую сторону, одного треугольника соответственно равны углу, стороне и высоте другого треугольника — такие треугольники равны.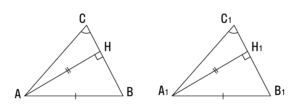

2. Если две стороны и медиана, заключенная между ними, одного треугольника соответственно равны двум сторонам и медиане другого треугольника — такие треугольники равны.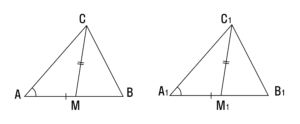

3. Если сторона и две медианы, проведенные к двум другим сторонам, одного треугольника соответственно равны стороне и двум медианам другого треугольника — такие треугольники тоже равны.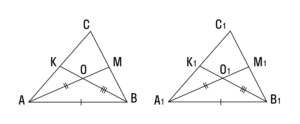

4. Если две стороны и биссектриса, заключенная между ними, одного треугольника соответственно равны двум сторонам и биссектрисе другого треугольника — такие треугольники тоже равны.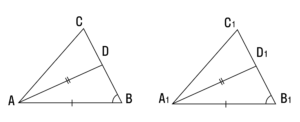

5. Два треугольника равны, если сторона, медиана и высота, проведенные к другой стороне, одного треугольника соответственно равны стороне, медиане и высоте другого треугольника.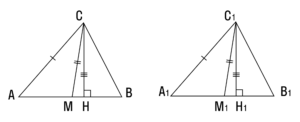

Все свойства треугольника можно посмотреть в статье: «Геометрия: свойства треугольника«.