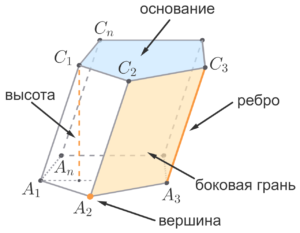
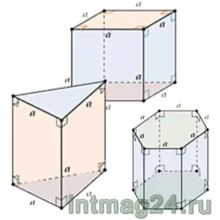
Призма – многогранник, две грани которого являются равными многоугольниками, лежащими в параллельных плоскостях, а остальные грани – параллелограммами, имеющими общие стороны с этими многоугольниками.
Равные грани (многоугольники) призмы называются её основаниями, а остальные грани — боковыми гранями. Рёбра боковых граней, не принадлежащие основаниям, называются боковыми рёбрами.
Свойства призмы:
- Основания призмы являются равными многоугольниками.
- Боковые грани призмы являются параллелограммами.
- Боковые ребра призмы параллельны и равны.
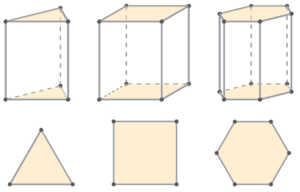
Виды призмы
В зависимости от количества сторон основания призмы отличают: треугольную, четырёхугольную, пятиугольную, шестиугольную и т. д. призмы.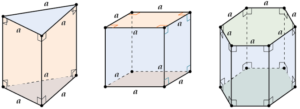 
Совокупность боковых граней призмы образуют боковую поверхность.
Площадь боковой поверхности призмы равна сумме площадей боковых граней.
Наклонная призма — призма, у которой боковые ребра не перпендикулярны основанию.
- Боковые грани – параллелограммы.
Прямая призма – призма, у которой все боковые ребра перпендикулярны основанию.
- Боковые грани прямой призмы — прямоугольники.
- В прямой призме боковые ребра являются высотами.
- Площадь боковой поверхности прямой призмы равна произведению периметра основания на длину бокового ребра (или, в данном случае, высоту призмы).
Призму, у которой основаниями являются параллелограммы, называют параллелепипедом.
Правильная призма – это призма, у которой все боковые грани – прямоугольники, а ее основания – правильные многоугольники.
Свойства правильной призмы:
- Основания правильной призмы являются правильными многоугольниками.
- Боковые грани правильной призмы являются равными прямоугольниками.
- Боковые ребра правильной призмы равны между собой.
- Правильная призма является прямой.
Формулы для призмы
Площадь полной поверхности призмы равна сумме площади её боковой поверхности и удвоенной площади основания: S = 2∙So + Sбок
Где: So — площадь основания, Sбок — площади всех боковых граней.
Объём призмы равен произведению площади основания призмы на её высоту: V = So∙h
Где: V — объем призмы, So — площадь основания, h – высота.
В случае куба и прямоугольного параллелепипеда формула объёма призмы: V=abc
Где: a,b,c, — длина, ширина и высота параллелепипеда.