Геометрия: свойства окружности и круга

Окружность — замкнутая плоская кривая, все точки которой одинаково удалены от данной точки (центра окружности), которая лежит в той же плоскости, что и кривая.

Круг — геометрическая фигура, состоящая из всех точек плоскости, расстояние от которых до точки O не превосходит R.

Определения для окружности и круга

Радиус — отрезок, который соединяет центр окружности с любой её точкой.
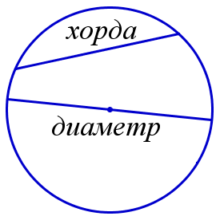
Хорда — отрезок, который соединяет какие-либо две точки окружности (AB).
Диаметр — хорда, проходящая через центр окружности(d).  Диаметр – наибольшая хорда окружности. Наименьшей хорды окружности не существует. 

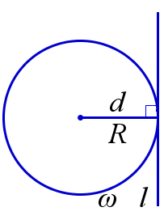
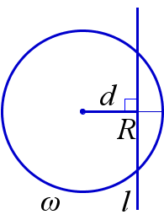
Касательная — прямая, которая лежит в одной плоскости с окружностью и имеет с ней только одну общую точку. Общая точка прямой и окружности называется точкой касания. В этом случае d=R.
Секущая — прямая, которая пересекает окружность в двух различных точках. В этом случае d<R.

Круговой сектор —  пересечение круга с плоским углом, вершина которого находится в центре этого круга.
Дуга окружности — геометрическая фигура, состоящая из всех точек окружности, принадлежащих некоторому плоскому углу с вершиной в центре этой окружности. Каждому такому углу соответствует ровно одна дуга окружности, и каждой дуге окружности соответствует ровно один плоский угол с вершиной в центре окружности.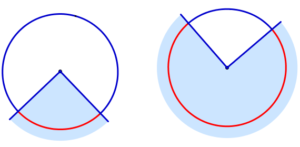

Круговой сегмент — пересечение круга с полуплоскостью, расстояние от границы которой до центра круга меньше радиуса этого круга. Если граница полуплоскости содержит центр круга, то соответствующий круговой сегмент называется полукругом.

Свойство хорды окружности

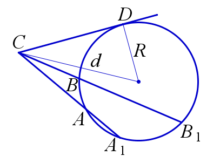
Произведения отрезков пересекающихся хорд равны между собой, т. е. ab = cd.
На рисунке: CA⋅CA1=CB⋅CB1=R2−d2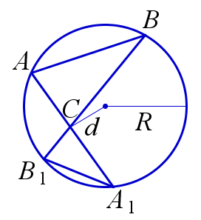

Свойства касательной окружности

Касательная к окружности перпендикулярна радиусу, проведённому в точку касания.

Свойства двух касательных из одной точки к окружности:
Пусть из точки A к окружности проведены две касательные AB1 и AB2 и O – центр окружности. Тогда:
1. AB1=AB2;
2. AO – биссектриса угла B1AB2;
3. OA – биссектриса угла B1OB2.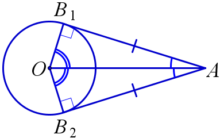

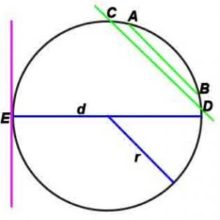
Свойство секущих к окружности

Теорема (о касательной и секущей). Если из одной точки к окружности проведены касательная и секущая, то квадрат отрезка касательной, соединяющего данную точку и точку касания, равен произведению отрезков секущей, соединяющих данную точку и точки ее пересечения с окружностью, т.е. a2 = bc. ИЛИ Квадрат касательной равен произведению секущей на ее внешнюю часть. На рисунке:
CD²=d²−R²
CD²=CA⋅CA₁=CB⋅CB₁

Если из точки, взятой вне окружности, к окружности проведено несколько секущих, то произведения больших отрезков секущих на их внешние части равны между собой. На рисунке: CA⋅CA₁=CB⋅CB₁

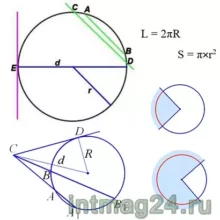
Основные формулы для окружности и круга:

Длина окружности: Площадь круга: или
где:
π= 3,14 (3,1415926535) – величина постоянная,
r-радиус,
d –диаметр,
L – длина окружности,
S-площадь.

Площадь кругового сектора

Площадь кругового сектора равна: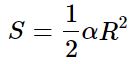 где α – радианная мера центрального угла, отвечающего данному сектору, R – радиус круга.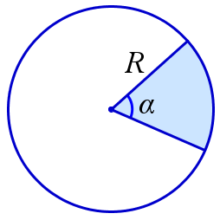

Площадь сегмента

Площадь кругового сегмента равна: 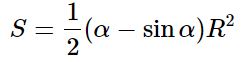где α – радианная мера центрального угла, отвечающего данному сегменту, R – радиус круга.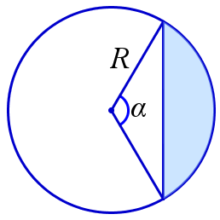

Калькулятор для окружности и круга поможет вычислить все характеристики круга по одной из известных величин.