Арифметическая прогрессия: понятие, свойства и формулы

Арифметическая прогрессия — это последовательность чисел (членов прогрессии), каждый член которой, начиная со второго, равен предыдущему члену с добавлением к нему одного и того же постоянного числа (шага или разности прогрессии).

Арифметическая прогрессия имеет вид:
а1, a1+d, a1+2d,…, a1+(n-1)d,…
где: d — разность арифметической прогрессии (шаг),
а1, a1+d, a1+2d,.. — члены арифметической прогрессии.

Если последовательность (a_n) является арифметической прогрессией, то для любого натурального значения n справедлива зависимость  a_n+1 = a_n + d.

Если известен первый член арифметической прогрессии a₁ и разность d, то возможно вычислить любой член арифметической прогрессии:
a₂ = a₁ + d;
a₃ = a₂ + d = a¹ +2d;
a₄ = a₃ + d = a₁ +3d;
и т. д.
n-ый член арифметической прогрессии можно получить, если к первому члену прогрессии добавить (n -1) разностей, т. е.,
a_n = a₁ + d(n−1),
где n — порядковый номер члена прогрессии, a₁ — первый член прогрессии, d — разность.

Шаг арифметической прогрессии вычисляется по формуле: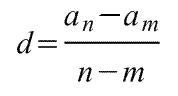

Формулы n-го члена арифметической прогрессии, если известны два соседних члена:
(любой член арифметической прогрессии, начиная со второго, является средним арифметическим предыдущего и следующего члена прогрессии)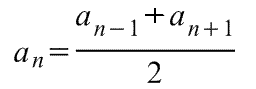

Формулы суммы арифметической прогрессии:

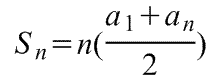или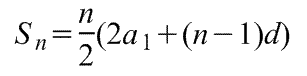

Пример.

Дана арифметическая прогрессия (a_n), где a₁ = 0 и d = 2. 
Написать: a) первые пять членов прогрессии; b) десятый член прогрессии; c) найти сумму первых пяти членов арифметической прогрессии.
Решение.

Чтобы найти последующий член прогрессии, нужно к предыдущему прибавить разность:
a₂ = a₁ + d = 0+2=2;
a₃ = a₂ + d = 2+2=4;
a₄ = a₃ + d = 4+2=6;
a₅ = a₄ + d = 6+2=8.

Чтобы найти десятый член арифметической прогрессии используется формула: a_n = a₁ + d(n−1).
Получаем: a₁₀ = a₁ + 2⋅(10−1) = 0 + 2⋅9 = 18.

Чтобы найти сумму арифметической прогрессии используется формула: S_n = n⋅(a₁+a_n)/2.
Получаем: S₅ = 5⋅(a₁+a₅)/2 = 5⋅(0+8)/2 = 20.

Для проверки правильности решения используйте Калькулятор арифметической прогрессии.

Читайте также «Геометрическая прогрессия: понятие, свойства, формулы«.