Задачи на совместную работу — это задачи, в которых несколько участников выполняют одну и ту же работу вместе, и нужно найти время, за которое они справятся с задачей. В таких задачах важно учитывать, что каждый участник вносит свой вклад, и их совместная работа ускоряет процесс.
Чтобы правильно решать задачи на совместную работу, нужно понять несколько ключевых понятий:
Производительность — это то, какую часть работы выполняет один участник за единицу времени (например, за час или минуту). Если один участник может выполнить всю работу за 4 часа, то его производительность равна 1/4 работы в час.
Общая производительность — это сумма производительностей всех участников. Когда несколько человек работают вместе, их усилия складываются, и общая работа выполняется быстрее.
Общее время работы — это время, которое потребуется всем участникам, чтобы выполнить работу вместе. Это время можно найти, разделив 1 (всю работу) на общую производительность.
Рассмотрим задачи на совместную работу:
Пример 1
Два друга, Маша и Коля, решили покрасить забор. Маша может покрасить весь забор за 6 часов, а Коля — за 3 часа. Сколько времени потребуется, чтобы они покрасили забор вместе?
Решение:
1. Определим производительность каждого:
Маша: за 1 час она красит 1/6 забора.
Коля: за 1 час он красит 1/3 забора.
2. Сложим их производительности, чтобы найти общую производительность:
Общая производительность: 1/6+1/3. Чтобы сложить дроби, приведём их к общему знаменателю: 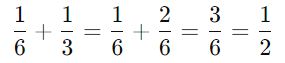
Значит, вместе они красят половину забора за 1 час.
3. Найдём общее время работы:
Если за 1 час они красят половину забора, то весь забор они покрасят за 2 часа.
Ответ: Маша и Коля покрасят забор вместе за 2 часа.
Пример 2
Две бригады работают над строительством дома. Первая бригада может построить дом за 12 дней, а вторая — за 8 дней. Сколько дней потребуется, чтобы они построили дом, работая вместе?
Решение:
1. Определим производительность каждой бригады:
Первая бригада: за 1 день они строят 1/12 дома.
Вторая бригада: за 1 день они строят 1/8 дома.
2. Сложим их производительности:
Общая производительность: 1/12+1/8. Найдём общий знаменатель: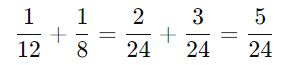
Это означает, что за 1 день обе бригады вместе строят 5/24 дома.
3. Найдём общее время работы:
Чтобы построить весь дом, потребуется: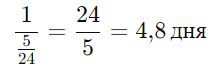
Ответ: Обе бригады вместе построят дом за 4,8 дня.
Заключение
Задачи на совместную работу учат нас находить баланс и понимать, как несколько человек, работая вместе, могут быстрее справиться с задачей. Важно помнить, что производительность каждого участника складывается, и для решения таких задач нужно просто правильно сложить дроби и найти общее время работы. Попробуйте решить несколько задач сами, чтобы лучше разобраться в этом!
Задачи по математике на совместную работу для самостоятельного решения:
Задача 1: Покраска забора
Два маляра, Андрей и Борис, работают вместе над покраской забора. Андрей может покрасить забор за 6 часов, а Борис — за 4 часа. Сколько времени потребуется, чтобы они покрасили забор вместе?
Задача 2: Наполнение бассейна
Две трубы могут наполнить бассейн вместе за 3 часа. Первая труба может наполнить его за 5 часов. Сколько времени потребуется, чтобы бассейн наполнился только через вторую трубу?
Задача 3: Работа на поле
Два фермера, Иван и Николай, вспахивают поле. Иван может вспахать всё поле за 8 часов, а Николай — за 12 часов. Сколько времени потребуется, чтобы они вспахали поле вместе?
Задача 4: Изготовление деталей
Два рабочих, Сергей и Павел, изготавливают детали. Сергей может изготовить одну деталь за 10 минут, а Павел — за 15 минут. Сколько времени потребуется, чтобы они вместе изготовили 12 деталей?
Задача 5: Сбор урожая
Два работника собирают яблоки в саду. Первый работник может собрать весь урожай за 9 часов, а второй — за 7 часов. За сколько часов они соберут урожай, работая вместе?
Решение к задачам для самостоятельного решения
Решение для задачи 1:
1. Найдем, какую часть забора красит каждый маляр за 1 час:
Андрей: 1/6 забора в час.
Борис: 1/4 забора в час.
2. Сложим их скорости: 1/6+1/4=5/12 забора в час.
3. Чтобы покрасить весь забор, нужно![]()
Ответ: Андрей и Борис покрасят забор вместе за 2,4 часа.
Решение для задачи 2:
1. Пусть x — время, за которое вторая труба наполняет бассейн.
2. Скорость первой трубы: 1/5 бассейна в час.
3. Совместная скорость: 1/3 бассейна в час.
4. Совместная скорость — это сумма скоростей обеих труб: 1/5+1/х=1/3.
5. Решим уравнение:![]()
6. x=15/2=7,5 часа.
Ответ: Вторая труба может наполнить бассейн за 7,5 часа.
Решение к задаче 3:
1. Найдем, какую часть поля вспахивает каждый фермер за 1 час:
Иван: 1/8 поля в час.
Николай: 1/12 поля в час.
2. Сложим их скорости: 1/8+1/12=5/24 поля в час.
3. Чтобы вспахать всё поле, нужно ![]()
Ответ: Иван и Николай вспашут поле вместе за 4,8 часа.
Решение к задаче 4:
1. Найдем, сколько деталей они изготавливают за 1 минуту:
Сергей: 1/10 детали в минуту.
Павел: 1/15 детали в минуту.
2. Сложим их скорости: 1/10+1/15=5/30=1/6 детали в минуту.
3. Чтобы изготовить 12 деталей, нужно ![]()
Ответ: Сергей и Павел вместе изготовят 12 деталей за 72 минуты.
Решение к задаче 5:
1. Найдем, какую часть урожая собирает каждый работник за 1 час:
Первый работник: 11/9 урожая в час.
Второй работник: 1/7 урожая в час.
2. Сложим их скорости: 1/9+1/7=16/63 урожая в час.
3. Чтобы собрать весь урожай, нужно![]()
Ответ: Оба работника вместе соберут урожай за примерно 3,94 часа.
