Найти сумму арифметической прогрессии

Сумма арифметической прогрессии — это сумма последовательных чисел, которые отличаются на одно и то же значение. Вот как её найти.

Формула суммы арифметической прогрессии

Сумма первых $n$ членов арифметической прогрессии (АП) может быть найдена с помощью следующей формулы:

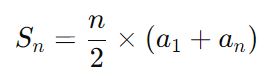
где:
S_n​ — сумма первых n членов,
n — количество членов прогрессии,
a₁ — первый член прогрессии,
a_n — последний член прогрессии.

Также можно использовать другую формулу, если известно, что: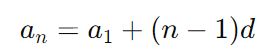

где d — разность прогрессии. Тогда сумма может быть представлена как: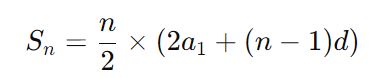

Пример 1: Простой расчет суммы

Допустим, у нас есть арифметическая прогрессия: 2,5,8,11,14

1. Определите параметры:
Первый член a₁=2
Последний член a_n=14
Количество членов n=5

2. Подставьте в формулу: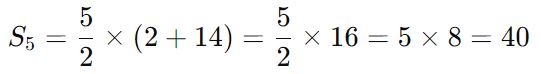

Ответ: Сумма первых 5 членов этой прогрессии равна 40.

Пример 2: Использование разности

Рассмотрим другую арифметическую прогрессию: 3,7,11,15,19.

1. Определите параметры:
a₁=3
d=7−3=4
n=5

2. Подставьте в формулу: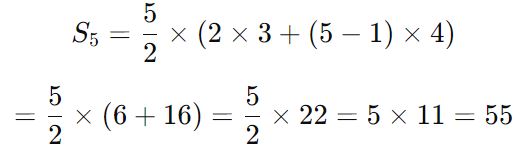

Ответ: Сумма первых 5 членов этой прогрессии равна 55.

Пример 3: Бесконечная арифметическая прогрессия

Обратите внимание, что бесконечная арифметическая прогрессия не имеет суммы, поскольку её члены не стремятся к определённому значению.

Заключение

Сумму арифметической прогрессии можно легко найти, используя формулы, основанные на количестве членов, первом и последнем членах прогрессии или разности. Если у вас есть конкретные данные или нужно проверить решение, используйте онлайн калькулятор арифметической прогрессии.