 Чтобы быстро решить задачи на движение, в том числе сложные и запутанные, нужно составить к ней схему или таблицу данных.
Чтобы быстро решить задачи на движение, в том числе сложные и запутанные, нужно составить к ней схему или таблицу данных.
- Схемы задач на движение помогают представить наглядно условие задачи и найти верное решение.
- Таблица к задачам на движение позволяет структурировать данные, чтобы наглядно видеть исходные данные и неизвестные величины.
Поэтому, чтобы решить сложные задачи на движение, нужно нарисовать схему, а в дополнение к схеме рекомендуется нарисовать таблицу, где в шапке параметры скорости, времени и расстояния. При этом везде применяется основная формула:![]()
 |
Скачать программы, которые формируют задачи на движение разных видов:
|
Рассмотрим решение следующих типов задач:
- простые задачи на скорость, время и расстояние;
- задачи на движение в разных направлениях: сближение и удаление;
- задачи на движение в одном направлении: сближение и удаление;
- решение задач на движение по реке.
Решить простые задачи на движение
Для решения простых задач на движение, как правило, схема или таблица не требуется, в них применяется формула нахождения скорости, времени или расстояния. Но иногда, чтобы не запутаться в решении, лучше воспользоваться каким-либо методом. Рассмотрим схему и таблицу, чтобы вы смогли выбрать наиболее удобный для себя способ разобраться в задаче.
Задача 1. Средняя скорость
Первые 5 часов автомобиль ехал со скоростью 60 км/ч, следующие 3 часа — со скоростью 100 км/ч, а последние 4 часа — со скоростью 75 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.
Решение.
Нарисуем схему движения.
Заполним все исходные данные в таблице. Также заполним другие ячейки таблицы по возможности (такие ячейки выделены зеленым цветом) 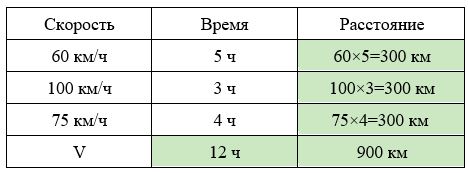
Средняя скорость — это отношение пройденного пути ко времени, за который пройден этот путь.
- Найдем общее расстояние: 900 км.
- Найдем время в пути: 5 + 3 + 4 = 12 часов.
- Найдем среднюю скорость автомобиля: 900:12 = 75 км/ч.
Задача 2. Движение с остановкой
В 9:00 велосипедист выехал из пункта А в пункт Б. Доехав до пункта Б, он сделал остановку на полчаса, а в 11:30 выехал обратно с прежней скоростью. В 13:00 ему оставалось проехать 8 км до пункта А. Найдите расстояние между пунктами А и Б.
Решение.
Нарисуем схему движения.
Заполним все исходные данные в таблице. Также заполним другие ячейки таблицы по возможности.
- Найдем скорость: 8 : 0,5 = 16 км/ч
- Найдем расстояние: 16×2=32 км.
Задача 3. Уровень ЕГЭ.
Лыжник планировал проехать 10 км с горы за 20 минут с постоянной скоростью v. Вместо этого первые несколько километров он проехал в два раза быстрее, чем планировал, а оставшиеся километры он проехал в два раза медленнее, чем планировал. В итоге весь путь занял у него 34 минуты. Сколько километров лыжник проехал в два раза быстрее, чем планировал?
Решение.
Нарисуем схему движения.
Заполним все исходные данные в таблице. Также заполним другие ячейки таблицы по возможности (такие ячейки выделены зеленым цветом) 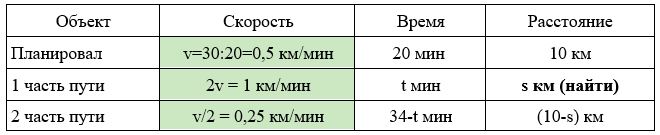
- Найдем скорость, с которой лыжник планировал скатиться: 10 : 20 = 0,5км/мин
- Найдем скорости, с которыми лыжник скатывался: 3км/мин и 0,25км/мин.
- Составим систему уравнений:
1) 1×t=s → t=s
2) 0,25×(34-t)=10-s → 0,25×(34-s)=10-s → s=2 км.
Решить задачи на движение в разных направлениях: сближение и удаление
Задача 4. Скорость удаления
Два автомобиля выехали одновременно из одного и того же пункта в противоположных направлениях. Скорость первого автомобиля 100 км/ч, скорость второго — 70 км/ч. Какое расстояние будет между автомобилями через 4 часа?
Решение.
Нарисуем схему движения.
Заполним все исходные данные в таблице. Также заполним другие ячейки таблицы по возможности (такие ячейки выделены зеленым цветом) /
Способ 1.
1) 100× 4 = 400 (км) — проехал первый автомобиль,
2) 70 × 4 = 280 (км) — проехал второй автомобиль.
3) 400 + 280 = 680 (км).
Способ 2.
1) (100 + 70), 170 км/ч — это скорость удаления автомобилей.
2) 170× 4 = 680 км.
Задача 5. Скорость сближения
Расстояние между городами А и В равно 750 км. Из города А в город В со скоростью 50 км/ч выехал первый автомобиль, а через три часа после этого навстречу ему из города В выехал со скоростью 70 км/ч второй автомобиль. На каком расстоянии от города А автомобили встретятся?
Решение.
Нарисуем схему движения.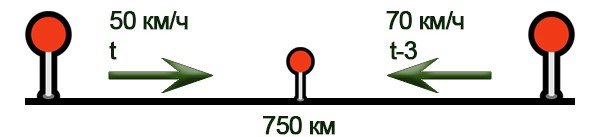
Заполним все исходные данные в таблице. Также заполним другие ячейки таблицы по возможности (такие ячейки выделены зеленым цветом)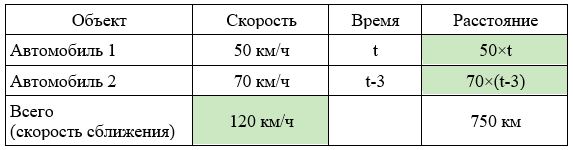
Способ 1.
- Составим уравнение: 50×t + 70×(t-3) =750
- Решим уравнение: 120t=960; t=8 часов.
- По условиям задачи нужно найти расстояние от пункта А, то есть расстояние для первого автомобиля: 50×8=400км.
Способ 2.
- За первые три часа пути автомобиль, выехавший из города А, проехал 150 километров и расстояние от него до города В стало равным 600 км.
- Скорость сближения двух автомобилей равна 120 км/ч, значит, они встретятся через 5 часов после выезда второго автомобиля: 600:120=5 часов.
- Таким образом, первый автомобиль всего ехал 8 часов: 50×8=400км.
Задача 6. Скорость сближения
Расстояние между пунктами А и В равно 135 км. Из пункта А в пункт В выехал легковой автомобиль. Одновременно с ним из пункта В в пункт А выехал грузовой автомобиль, скорость которого на 15 км/ч меньше скорости легкового. Через час после начала движения они встретились. Через сколько минут после встречи грузовой автомобиль прибыл в пункт А?
Решение.
Нарисуем схему движения.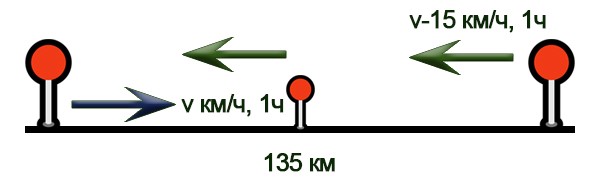
Заполним все исходные данные в таблице. Также заполним другие ячейки таблицы по возможности (такие ячейки выделены зеленым цветом)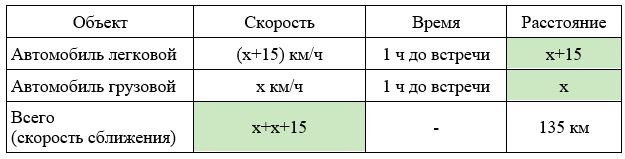
- Пусть x км/ч — скорость грузового автомобиля, тогда (x + 15) км/ч — скорость легкового автомобиля. Получаем уравнение: x+x+15=135; x=60км/ч.
- Найдем сколько времени грузовой автомобиль затратил на весь путь: 135:60=2,25 часов.
- Найдем сколько времени грузовой автомобиль затратил на путь после встречи: 2,25-1=1,25 часов или 75 минут (1,25*60).
- Ответ: 75 мин.
Задача 7. Уровень ЕГЭ.
Два поезда движутся навстречу друг другу – один со скоростью 70 км/ч, другой со скоростью 80 км/ч. Пассажир, сидящий во втором поезде, заметим, что первый поезд прошел мимо него за 12 секунд. Какова длина первого поезда? Ответ дайте в метрах.
Решение.
Заполним все исходные данные в таблице. Также заполним другие ячейки таблицы по возможности (такие ячейки выделены зеленым цветом) 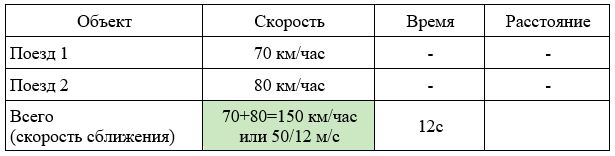
- Найдем скорость сближения: 70+80=150км/ч.
- Переведем ее в другие единицы измерения: 150 км/ч = 150000/3600 = 50/12 м/с
- Заметим, что фраза “первый поезд прошел мимо пассажира за 12с” означает, что с того момента, как пассажир увидел голову поезда, до того момента, как он увидел хвост поезда, прошло 12с.
- Найдем расстояние 50/12 × 12 =50 метров.
Решить задачи на движение в одном направлении: сближение и удаление
Задача 8. Скорость сближения
Поезд, двигаясь равномерно со скоростью 63 км/ч, проезжает мимо идущего в том же направлении параллельно путям со скоростью 3 км/ч пешехода за 57 секунд. Найдите длину поезда в метрах.
Решение.
Нарисуем схему движения.
Заполним все исходные данные в таблице. Также заполним другие ячейки таблицы по возможности (такие ячейки выделены зеленым цветом)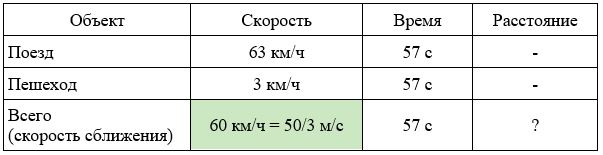
- Найдем скорость поезда относительно пешехода: 63 − 3 = 60 км/ч
- Переведем скорость сближения в другие единицы измерения: 60 км/ч = 60000/3600=50/3 м/с.
- Найдем длину поезда (расстояние, которое проехал поезд): (50/3)*57=950 м.
Задача 9. Скорость сближения
Два туриста одновременно вышли в одном направлении в город N. При этом вышли они из разных городов, расстояние между которыми 9 км. Известно, что турист, изначально находившийся дальше от города N, шёл со скоростью, в два раза превышающей скорость другого туриста. В город N они прибыли одновременно, через 3 часа после начала движения. Найдите скорость туриста, который шёл быстрее. Ответ дайте в км/ч.
Решение.
Нарисуем схему движения.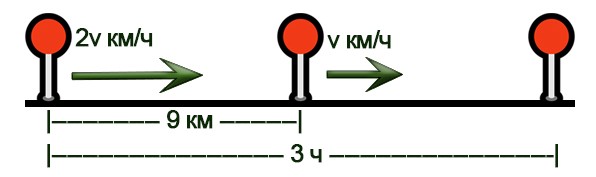
Заполним все исходные данные в таблице. Также заполним другие ячейки таблицы по возможности (такие ячейки выделены зеленым цветом) 
- Найдем скорость сближения туристов: 9:3=3 км/ч.
- По формуле сближения получаем: 2v-v=3 → v=3 →2v=6 км/ч.
- Ответ: 6
Задача 10. Скорость удаления
Два велосипедиста выехали из одного места в одном направлении. Скорость первого – 10 км/ч, а второго – 18 км/ч. Через сколько часов расстояние между велосипедистами будет равно 104 км?
Решение.
Нарисуем схему движения.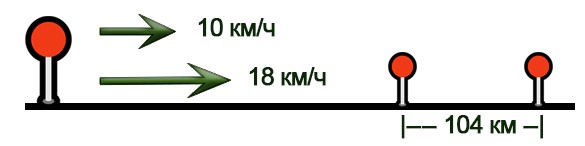
Заполним все исходные данные в таблице. Также заполним другие ячейки таблицы по возможности (такие ячейки выделены зеленым цветом)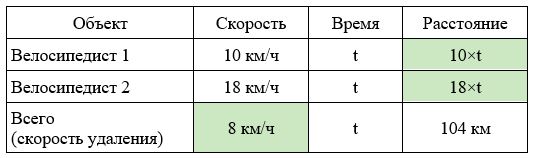
- Найдем скорость удаления: 18-10=8 км/ч
- Найдем время в пути: 108:8=13 часов.
- Ответ: 13
Задача 11. Скорость удаления
Два велосипедиста выехали в одном направлении из мест, находящихся на расстоянии 13 км друг от друга. Скорость первого – 12 км/ч, а второго – 17 км/ч, причем второй находился в начале движения впереди. Через сколько часов расстояние между велосипедистами будет равно 58 км?
Решение.
Нарисуем схему движения.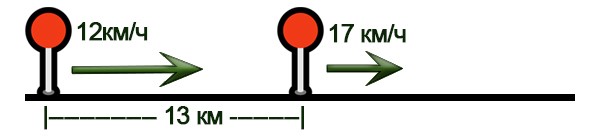
Заполним все исходные данные в таблице. Также заполним другие ячейки таблицы по возможности (такие ячейки выделены зеленым цветом)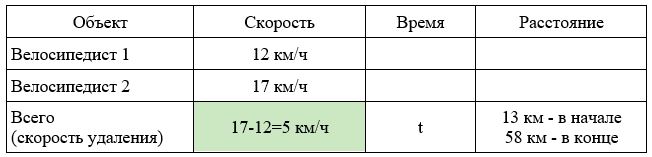
- Найдем скорость удаления: 17-12=5 км/ч
- Найдем расстояние, на которое они удались друг от друга: 58-13=45 км.
- Найдем время: 45:5=9 часов.
Задача 12. Уровень ЕГЭ
Два кота одновременно выбегают в одном направлении из одного и того же подъезда. Скорость первого на 0,5 км/ч больше скорости второго. Через сколько минут расстояние между котами станет равным 200 метрам?
Решение.
Заполним все исходные данные в таблице. Также заполним другие ячейки таблицы по возможности (такие ячейки выделены зеленым цветом)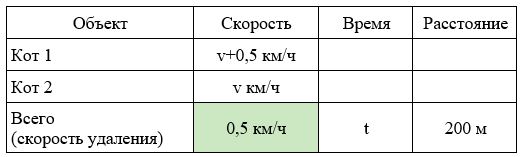
- Скорость удаления будет 0,5 км/ч — это скорость, с которой первый кот бежит быстрее второго.
- Найдем время: 0,2 : 0,5 = 0,4 часа
- Переведем время в другие единицы измерения: 0,4 ч = 0,4*60 = 24 мин.
Решить задачи на движение по реке
Задача 13.
Яхта движется по стоячей воде, ее собственная скорость равна 30 км/ч. Встречный ветер каждую минуту сносит яхту на 20 метров. За сколько часов яхта пройдет 259200 метров?
Решение.
Заполним все исходные данные в таблице. Также заполним другие ячейки таблицы по возможности (такие ячейки выделены зеленым цветом) 
- Переведем скорость яхты в другие единицы измерения: 30 км/ч = 500 м/с.
- Найдем скорость удаления: 500-20=480 м/с.
- Найдем время: 259200 :480=540 минут = 9 часов.
Задача 14.
Расстояние от пристани А до пристани Б по течению реки катер прошёл за 5 часов, а на обратный путь он затратил на 1 час больше. Найдите скорость катера в неподвижной воде (собственную скорость), если скорость течения реки 2 км/ч.
Решение.
Заполним все исходные данные в таблице. Также заполним другие ячейки таблицы по возможности (такие ячейки выделены зеленым цветом) 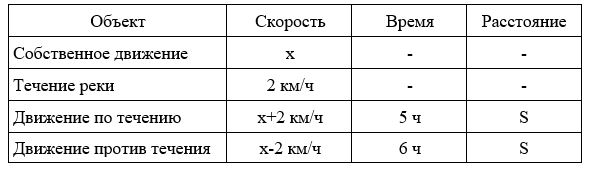
- Пусть скорость катера в неподвижной воде равна x км/ч.
- Составим уравнение: 5×(x+2)=6×(x-2); x=22 км/ч.
 |
Скачать программы, которые формируют задачи на движение разных видов:
|
Правильность решения задач вы можете проверить на сайте intmag24.ru с помощью калькулятора решения задач на движение.
Советы для решения задач на движения
- В процессе решения задач на движение может быть составлена формула квадратного уравнения, которое будет иметь два корня. В этом случае нужно взять тот ответ, который будет логичен для задачи (положительный). Отрицательный корень не берется во внимание.
- Внимательно следите, чтобы в задаче все данные измерялись одними величинами. Если это не так, нужно се привести к единым единицам измерения.
