Геометрия: свойства трапеции

Трапеция — четырёхугольник, у которого только две противолежащие стороны параллельны.

При этом трапеция обладает всеми свойствами четырехугольника.  Поэтому запоминать надо свойства, которые характерны для трапеции.

Определения для трапеции:

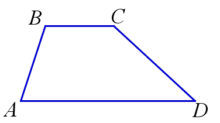Параллельные стороны называются основаниями трапеции (BC и AD), непараллельные – боковыми сторонами (AB и CD).

Высота трапеции – перпендикуляр, проведённый из произвольной точки одного основания трапеции к прямой, содержащей другое основание трапеции.  

Средняя линия трапеции — отрезок, который соединяет середины боковых сторон данной трапеции (на рис. MN). Средняя линия трапеции параллельна её основаниям и равна их полусумме. Средняя линия параллельна основаниям. Её длина находится по формуле:  MN=(AD+BC)/2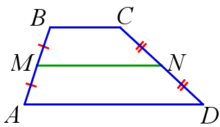
M – середина AB, N – середина CD,
AD||BC, MN||AD, MN||BC,

Равнобедренная (равнобокая) трапеция – трапеция, у которой боковые стороны равны (AB=CD).
В равнобедренной трапеции:
— углы при основании равны,
— проекции боковых сторон на основание равны: AE=FD,
— диагонали равны.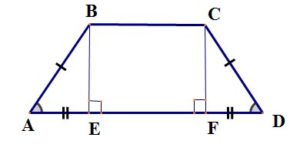

Прямоугольная трапеция — трапеция, у которой одна из её боковых сторон перпендикулярна основаниям.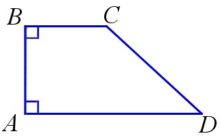

Свойства углов трапеции

Свойства углов четырехугольника

➜ Сумма углов трапеции равна 360°
➜ Сумма внешних углов трапеции , взятых по одному при каждой вершине, равна 360°.
➜ Каждый угол трапеции всегда меньше суммы трёх остальных углов.

Свойства углов  трапеции 

1. Сумма углов, прилежащих к боковой стороне, равна 180°: ∠A+∠B=180°, ∠C+∠D=180°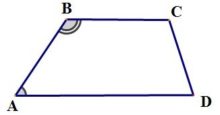

2. Каждая диагональ трапеции образует с её основаниями равные углы.
3.  Биссектриса любого угла трапеции отсекает на ее основании отрезок, равный боковой стороне: AB=BE.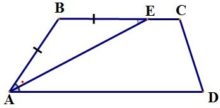

4. Биссектрисы смежных углов трапеции пересекаются под прямым углом.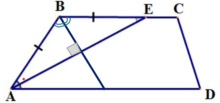

Свойства сторон трапеции

Свойства сторон трапеции (как у четырехугольника)
➜ Каждая сторона четырехугольника меньше суммы всех его других сторон.
➜ Сумма диагоналей меньше его периметра.

Диагонали трапеции (как у четырехугольника)
➜ Диагонали пересекаются в одной точке.
➜ Произведение диагоналей вписанного четырёхугольника равно сумме произведений противоположных сторон.
➜ Две противоположные стороны четырёхугольника перпендикулярны тогда и только тогда, когда сумма квадратов двух других противоположных сторон равна сумме квадратов диагоналей.
➜ Диагонали четырёхугольника перпендикулярны тогда и только тогда, когда суммы квадратов противоположных сторон равны.

При пересечении диагоналей трапеции и продолжений её боковых сторон образуются подобные треугольники, прилежащие к основаниям.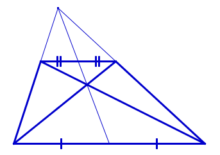

Трапеция и окружность

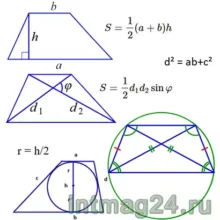
В трапецию можно вписать окружность, если сумма её оснований равна сумме боковых сторон (a+b=c+d). Центром вписанной в трапецию окружности является точка пересечения биссектрис внутренних углов трапеции.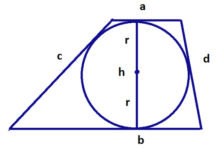Радиус вписанной окружности:

Окружность можно описать около трапеции тогда и только тогда, когда трапеция является равнобедренной. Центр описанной около трапеции окружности является точкой пересечения всех четырёх серединных перпендикуляров сторон.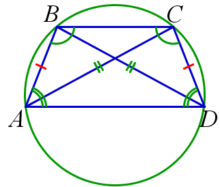
AB=CD ⇒ ∠ABC=∠DCB, ∠BAD=∠CDA;
AB=CD ⇒ AC=BD;
AB=CD ⇒ ABCD вписанная

Основные формулы:

Периметр трапеции равен сумме длин всех его сторон:

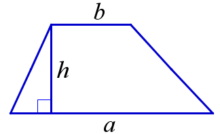
Площадь трапеции можно найти по двум формулам:

1.  Половине произведения суммы её оснований на высоту трапеции.

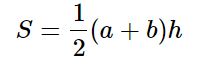2. Половине произведения её диагоналей на синус угла между ними.

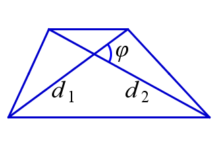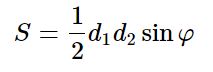Площадь трапеции можно найти с помощью онлайн калькулятора площади трапеции.

Стороны и диагональ равнобокой трапеции: 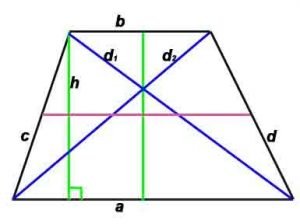Расшифровка:
 a,b — основания,
c,d — боковые стороны (с – боковые стороны в случае, если трапеция равнобокая),
d₁, d₂ –диагонали,
P-периметр,
S-площадь,
h -высота, проведенная к противоположной стороне

Скачать программы, которые формируют задания на нахождение периметра и площади геометрических фигур, а также неизвестных характеристик (сторон, диагоналей и др.), в том числе для: квадрата, прямоугольника, треугольника, трапеции и другие.