Геометрическая прогрессия — последовательность чисел b1, b2, b3,.. (членов прогрессии), в которой каждое последующее число, начиная со второго, получается из предыдущего умножением его на определённое число q (знаменатель прогрессии), где b1≠0 , q≠0.
Геометрическая прогрессия имеет вид:
b1, b2=b1q, b3=b2q, …, bn=bn-1q…
где: q — знаменатель геометрической прогрессии (шаг),
b1, b2, b3, …, bn,.. — члены геометрической прогрессии.
n-й член геометрической прогрессии bn определяется по формуле:
bn=b1⋅qn-1
- Если b1 > 0 и q > 1 — прогрессия является возрастающей,
- Если 0 < q < 1 — прогрессия является убывающей,
- Если q < 0 — прогрессия является знакопеременной.
Формулы суммы первых n членов геометрической прогрессии:
При q < 1 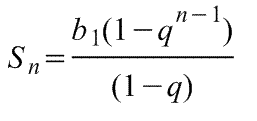
При q > 1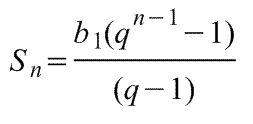
Формула суммы бесконечной геометрической прогрессии:
При -1 < q < 1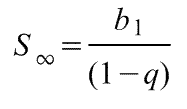
Говорят, что бесконечная геометрическая прогрессия сходится, если предел lim Sn при n→∞ существует и конечен. В противном случае прогрессия расходится.
Свойства геометрической прогрессии
Модуль любого члена геометрической прогрессии, кроме первого, равен среднему геометрическому (среднему пропорциональному) двух рядом с ним стоящих членов (при n>2). ![]()
Знаменатель геометрической прогрессии рассчитывается по формуле: 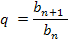
Произведение членов, равноудаленных от краев геометрической прогрессии, то есть, соседних, всегда является постоянной величиной: ![]()
Читайте также «Арифметическая прогрессия: понятие, свойства, формулы«.
