Задачи с параметрами — это математические задачи, в которых одно или несколько условий зависят от какого-то параметра (обычно это переменная, обозначенная буквой, например, a, k, m и т.д.). Основная цель таких задач — найти, при каких значениях параметра решение существует, а при каких — нет, или сколько решений имеет задача в зависимости от параметра.
Общий алгоритм решения задач с параметрами
1. Анализ условий задачи. Прочитать условия задачи и понять, что требуется найти. Чаще всего это нахождение значения параметра, при котором уравнение/неравенство/система имеет решения или имеет определённые свойства (например, одно решение, два решения, бесконечно много решений, и т.д.).
2. Постановка задачи в общем виде. Подставить все условия задачи и записать её в виде уравнения или системы уравнений с параметром. Это даст общую форму задачи, с которой можно работать.
3. Исследование уравнения или системы. Рассмотреть различные возможные случаи для параметра:
➤ Найти дискриминант (если уравнение квадратичное).
➤ Рассмотреть условия существования корней (если это логарифмы, корни или дробные выражения).
➤ Исследовать функцию (если задача связана с функциями или их графиками).
4. Выражение параметра. Найти значение параметра, при котором выполняется условие задачи. Иногда это требует рассмотрения нескольких случаев, так как разные значения параметра могут давать разные результаты.
5. Проверка всех возможных решений. Убедиться, что найденные решения соответствуют всем условиям задачи (например, что корни лежат в допустимой области).
Пример 1: Квадратное уравнение с параметром
Задача: Найти, при каких значениях параметра a квадратное уравнение ax2+(2a−1)x+a−1=0 имеет два различных корня.
Решение:
1. Анализ задачи. Уравнение имеет два различных корня, если его дискриминант больше нуля.
2. Дискриминант квадратного уравнения.
Для уравнения ax2+(2a−1)x+a−1=0, коэффициенты:
A=a, B=2a−1, C=a−1.
Дискриминант D выражается как:
D=B2−4AC=(2a−1)2−4a(a−1)
Вычислим дискриминант:
D=(2a−1)2−4a(a−1)=4a2−4a+1−4a2+4a=1
3. Анализ дискриминанта. D=1, и это всегда положительное число. Это значит, что для любого значения a дискриминант больше нуля, а значит, уравнение всегда имеет два различных корня.
Ответ: Уравнение имеет два различных корня при любом a∈R.
Пример 2: Условие существования решений уравнения с параметром
Задача: Найти, при каких значениях параметра k уравнение √(2x−1)=kx имеет хотя бы одно решение.
Решение:
1. Анализ задачи. Чтобы уравнение √(2x−1)=kx имело решение, нужно учитывать область определения: подкоренное выражение должно быть неотрицательным, а правая часть должна быть определена для соответствующих значений .
Условия: 2x−1≥0 ⇒ x≥1/2.
2. Решение уравнения. Возведём обе части в квадрат:![]() Приведём уравнение к стандартному виду:
Приведём уравнение к стандартному виду:
k2x2−2x+1=0
Это квадратное уравнение относительно x.
3. Исследование дискриминанта. Чтобы уравнение имело решение, дискриминант должен быть неотрицательным:
D=(−2)2−4⋅k2⋅1=4−4k2
Условие существования решений:
D≥0 ⇒ 4−4k2 ≥0 ⇒ k2≤1
Следовательно, −1≤ k ≤1
4. Проверка условий. Мы выяснили, что решение существует, если k2≤1, то есть k∈[−1,1].
Ответ: Уравнение имеет хотя бы одно решение при k∈[−1,1].
Пример 3: Система уравнений с параметром
Задача: Найти все значения параметра aa, при которых система уравнений имеет решение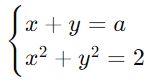
Решение:
1. Из первого уравнения выразим y: y=a−x
2. Подставим это выражение во второе уравнение: x2+(a−x)2=2
Раскроем скобки:
x2+(a2−2ax+x2)=2 ⇒ 2x2−2ax+a2 =2
Приведём уравнение к стандартному виду: ![]()
3. Исследуем дискриминант этого квадратного уравнения относительно x:
Дискриминант:
D=(−2a)2−4⋅2⋅(a2−2) = 4a2−8(a2−2) = 4a2−8a2+16 = −4a2+16
Чтобы уравнение имело решение, дискриминант должен быть неотрицательным:
−4a2+16≥0 ⇒ a2≤4
Следовательно, a∈[−2,2].
Ответ: Система имеет решение при a∈[−2,2].
