Равномерное движение тела (точки) по окружности является частным случаем криволинейного движения. Оно представляет собой вращение какой-либо материальной точки или тела относительно оси, неподвижной в выбранной системе с постоянной угловой скоростью.
Равномерное движение тела (точки) по окружности — движение тела (точки) с постоянной по модулю скоростью (ν = const) по траектории, представляющей собой окружность.
Формулы для равномерного движения тела по окружности
Для описания такого перемещения применяют следующие формулы: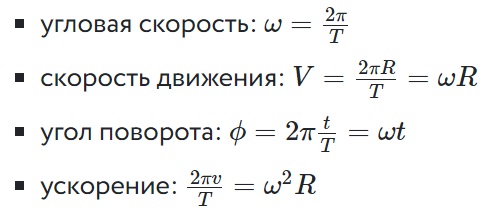
Где:
Т — период вращения;
t — время;
ω — угловая скорость;
R — радиус;
at — тангенциальное ускорение;
an — центростремительное или полное ускорение.
При отсутствии специальных оговорок, в процессе решения задач движение тела по окружности принимают за равномерное. Для расчета расстояния, скорости и времени используют следующие формцлы: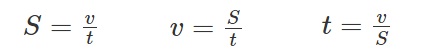 
где:
S — расстояние, которое преодолело тело;
v — скорость движения тела;
t — время движения.
Скорость при движении тела (точки) по окружности
Скорость тела (точки) направлена по касательной к окружности в каждый момент времени. Ее называют линейной скоростью (v). При таком движении скорость точки меняется по направлению, а по модулю остается неизменной.
Равномерное движение точки по окружности является движением с ускорением (a).
Ускорение всегда направлено к центру окружности и называется центростремительным или нормальным. Модуль центростремительного ускорения определяется формулой: 
где: v — линейная скорость, R — радиус окружности.
При решении задач на равномерное движение тела (точки) по окружности часто используют такие величины, как радиус, угол поворота и угловая скорость. Угловая скорость (w) показывает, на сколько изменяется угол поворота (измеряется в радианах/секунду) за время (t): 
Если период обращения — T, частота обращения — v, то угловая скорость выражается по формулам:
— Отношение угловой скорости (w) и линейной скорости (v) при движении по окружности
— Отношение угловой скорости (w) и модуля центростремительного ускорения (a)
Используя предыдущие формулы, можно вывести следующие соотношения: 
Решение задач на равномерное движение тела по окружности
Задача 1
Длина круговой трассы равна 8 километров. Из ее точки в один момент времени в одинаковом направлении выехали два автомобиля. Первый автомобиль развил скорость 114 км/ч и, спустя 20 минут после начала движения, обогнал второй автомобиль на один круг. Требуется определить скорость, с которой двигался второй автомобиль. Ответ необходимо представить в км/ч.
Решение.
Известно, что через 20 минут после начала движения первое транспортное средство опережало второе на один круг. Значит, в течение 20 минут первый автомобиль преодолел на 1 круг больше, то есть на 8 км больше. За час первый автомобиль проехал на 8*3=24 км больше, чем второй. Скорость второго транспортного средства на 24 км/ч меньше по сравнению с первым, и равна 114-24=90 км/ч.
Ответ: второй автомобиль двигался со скоростью 90 км/ч.
Задача 2
Из пункта А круговой трассы выехал велосипедист, а спустя полчаса стартовал мотоциклист. Через 10 минут после начала пути водитель мотоцикла догнал велосипедиста в первый раз. Спустя еще 30 минут мотоциклист догнал велосипедиста повторно. Требуется определить, какова скорость мотоциклиста, в том случае, когда длина трассы составляет 30 км. Ответ необходимо представить в км/ч.
Решение.
В первую очередь требуется перевести минуты в часы. Скорости мотоциклиста и велосипедиста можно обозначить х и у. В первый раз водитель мотоцикла обогнал велосипедиста, спустя 10 минут или 1/6 часа после начала движения. До этого момента велосипедист находился в движении 40 минут или 2/3 часа.
Можно упростить запись условий задачи:
велосипедист: v = х, t = 2/3, S = 2/3*х;
мотоциклист: v = у, t = 1/6, S = 1/6*у.
Велосипедист и мотоциклист преодолели одинаковый путь: 16y=23x
Спустя 30 минут или 1/2 часа после первого обгона мотоциклист выполнил второй обгон велосипедиста.
Таким образом:
велосипедист: v = х, t = 1/2, S = 1/2*х;
мотоциклист: v = у, t = 1/2, S = 1/2*у.
Требуется определить расстояния, которые преодолели гонщики. Мотоциклист обогнал велосипедиста, то есть проехал больше на один круг. Это является ключевым моментом в данной задаче. Один круг составляет 30 километров. Второе уравнение будет иметь вид: 12y−12x=30
Далее необходимо решить полученную систему: у = 4х и у – х = 60.
Таким образом, х = 20, у = 80.
Ответ: скорость мотоциклиста равна 80 км/ч.
Задача 3
На часах со стрелками время 8 часов 00 минут. Требуется определить, через сколько минут минутная стрелка в четвертый раз догонит часовую стрелку.
Решение.
Спустя один час минутная стрелка преодолевает один круг, а часовая проходит лишь 1/12 циферблата. Допустим, что скорости равны 1 круг в час и 1/12 круга в час соответственно. Начало движения приходится на 8.00. Необходимо определить время, в течение которого минутной стрелке в первый раз удастся догнать часовую.
Минутная стрелка преодолеет на 2/3 круга больше. Исходя из этого, можно записать уравнение: 1∗t−112t=23.
Таким образом, спустя 8/11 часа стрелки совпадут. Предположим, что через время z стрелки совпадут повторно. Минутная стрелка преодолеет расстояние 1*z, а часовая 1/12*z. При этом минутной стрелкой будет пройдено на один круг больше. Можно записать уравнение: 1∗z−112z=1
Решение данного уравнения будет таким: z=1211
Таким образом, через 12/11 часа стрелки совпадут повторно. Спустя еще 12/11 часа они встретятся вновь и так далее. Поэтому при старте в 8.00 в четвертый раз минутная стрелка догонит часовую через: 811+31211
часа.
Ответ: минутная и часовая стрелки совпадут в четвертый раз через 811+31211 часа.