Задачи на скорость, время и расстояние часто используются для решения задач, связанных с движением. Вот несколько типичных примеров таких задач:
Простая задача на движение:
В таким задачах просто используется формула для определения неизвестной величины.
Автомобиль проехал 240 км за 4 часа. Найдите скорость автомобиля.
Решение: Используем формулу S=V×t, где:
- — расстояние,
- — скорость,
- t — время.
Чтобы найти скорость, нужно разделить расстояние на время: V=S/t=240/4=60 км/ч.
Задача на встречное движение
В таких задачах два объекта движутся навстречу друг другу.
Задачи на встречное движение можно решать двумя способами:
1. Найти значения скорости, времени и расстояния для каждого объекта.
2. Найти скорость сближения объектов (как сумму их скоростей), общие время и расстояние.
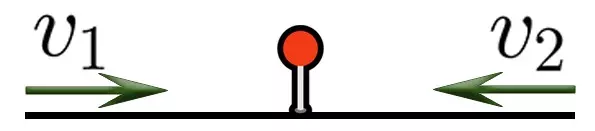
Задача: Два поезда отправились одновременно навстречу друг другу из двух городов, расстояние между которыми 600 км. Один поезд движется со скоростью 70 км/ч, другой — со скоростью 80 км/ч. Через сколько времени они встретятся?
Решение: Время можно найти, разделив расстояние на суммарную скорость поездов:
- Vобщ=70+80=150 км/ч.
- Тогда время до встречи: t=600/150=4 часа.
Задача на удаление
В таких задачах два объекта движутся в противоположных направлениях, удаляясь друг от друга.
В таком типе задачи используется скорость удаления. Задачи на движение в противоположных направлениях также можно решить двумя способами:
1. Найти значения скорости, времени и расстояния для каждого объекта.
2. Найти скорость удаления объектов (как сумму их скоростей), общие время и расстояние.
Задача: Два поезда отправились одновременно выехали из одного города в противоположных направлениях. Один поезд движется со скоростью 60 км/ч, другой — со скоростью 70 км/ч. Какое расстояние будет между ними через 3 часа?
Решение: Расстояние можно найти, умножив время на суммарную скорость поездов:
- Vобщ=60+70=130 км/ч.
- Тогда расстояние через 3 часа: S=130×3=390 км.
Задача на движение в одном направлении
В таких задачах два объекта движутся в одном направлении с разной скоростью, при этом они сближаются друг с другом или отдаляются друг от друга.
Соответственно находится:
- скорость сближения — когда один объект догоняет второй
- скорость удаления — когда один объект отстает от второго.
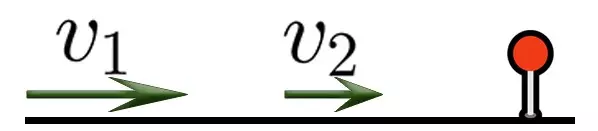

Задача: Велосипедист и пешеход движутся в одном направлении. Скорость велосипедиста 18 км/ч, а пешехода — 6 км/ч. Через сколько часов велосипедист догонит пешехода, если между ними 24 км?
Решение: Чтобы найти время, нужно разделить расстояние на разность скоростей:
- Vразн=18−6=12 км/ч.
- Время: t=24/12=2 часа.
Задача на движение по течению и против течения
- Чтобы узнать скорость объекта, который движется по течению реки, надо к собственной скорости объекта прибавить скорость течения реки.
- Чтобы узнать скорость объекта, который движется против течения реки, надо из собственной скорости объекта вычесть скорость течения реки.
Лодка плывет по реке. Скорость лодки в стоячей воде — 10 км/ч, скорость течения — 2 км/ч. Какое расстояние пройдет лодка за 3 часа по течению и за 3 часа против течения?
Решение:
- Скорость по течению: 10+2=12V км/ч.
Расстояние по течению: 12×3=36 км. - Скорость против течения: 10−2=8 км/ч.
Расстояние против течения: 8×3=24 км.
Общий путь: 36+24=60 км.
Эти задачи помогут вам попрактиковаться в использовании формул для нахождения скорости, времени и расстояния.
Внимательно следите, чтобы в задаче все данные измерялись одними величинами. Если это не так, нужно се привести к единым единицам измерения. Используйте конвертеры для перевода:
- Конвертер единиц измерения скорости
- Конвертер единиц измерения времени
- Конвертер единиц измерения расстояния (длины)
Для проверки задач используйте онлайн калькулятор решения задач на движение.
 |
Скачать программы, которые формируют задачи на движение разных видов: |
