Формулы сокращённого умножения со степенями — это набор алгебраических тождеств, которые позволяют упростить операции с многочленами. Эти формулы часто используются для раскладывания многочленов на множители или для быстрого возведения в квадрат и куб. Рассмотрим каждую формулу подробно, с объяснением и примерами.
1. Квадрат суммы:
![]()
Эта формула используется для возведения суммы двух чисел или переменных в квадрат. В правой части формулы результат складывается из трёх членов: квадрата первого числа (или переменной), удвоенного произведения двух чисел и квадрата второго числа.
Пример: (x+5)2 = x2+2⋅x⋅5+52 = x2+10x+25
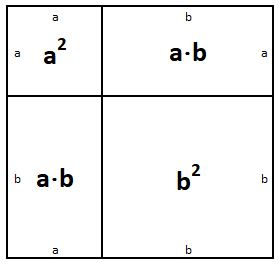
Графическая иллюстрация:
Представьте квадрат с длинами сторон (a+b). Его площадь — это сумма квадратов сторон и двух прямоугольников с площадями a⋅b. Получаем:
(a+b)2=a2+2⋅a⋅b+b2
2. Квадрат разности:
![]()
Эта формула похожа на квадрат суммы, но здесь вместо суммы рассматривается разность. Отличие только в том, что знак перед произведением 2ab становится отрицательным.
Пример: (x−4)2 = x2−2⋅x⋅4+42 = x2−8x+16
Графическая иллюстрация:
Если вы представите квадрат с длиной стороны (a−b), то его площадь будет равна как разность площади большого квадрата — а2 и площадей двух прямоугольников — b⋅(a-b). Получаем:
(a-b)2=a2— 2⋅b⋅(a-b) -b2 = a2— 2⋅a⋅b + 2⋅b2 — b2 = a2— 2⋅a⋅b + b2.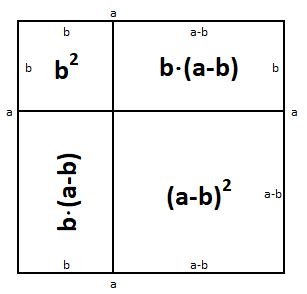
3. Разность квадратов:
![]()
Эта формула показывает, что разность квадратов двух чисел можно разложить на произведение разности и суммы этих чисел. Это важное тождество часто используется для факторизации выражений.
Пример: x2−9=(x−3)(x+3)
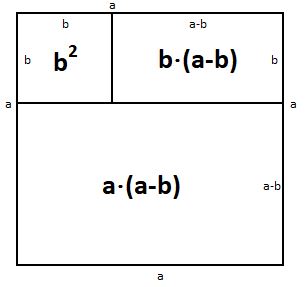
Графическая иллюстрация:
Если у вас есть два квадрата с длинами сторон a и b, их разность можно представить как сумму площадей двух разных прямоугольников: a2-b2 = b⋅(a-b) + a⋅(a-b).
Сгруппируем слагаемые и получим: a2-b2 = (a+b)⋅(a-b)
4. Куб суммы:
![]()
Эта формула используется для возведения суммы двух чисел или переменных в куб. В правой части присутствуют четыре члена: куб первого числа, трижды произведение квадрата первого числа на второе, трижды произведение первого числа на квадрат второго, и куб второго числа.
Пример: (x+2)3 = x3+3⋅x2⋅2+3⋅x⋅22+23 = x3+6x2+12x+8
Графическая иллюстрация:
Представьте трёхмерный куб с длинами сторон a+b. Его объём состоит из объёмов нескольких частей: куба первого числа, куба второго числа и объёмов нескольких прямоугольных параллелепипедов.

5. Куб разности:
![]()
Аналогично кубу суммы, эта формула описывает куб разности. Разница лишь в том, что знаки произведений меняются на противоположные.
Пример: (x−3)3=x3−3⋅x2⋅3+3⋅x⋅32−33=x3−9x2+27x−27
Графическая иллюстрация:
Представьте разницу объёмов трёхмерных фигур — кубов, которые пересекаются, при этом часть объёма будет отрицательной.
6. Сумма кубов:
![]()
Эта формула помогает разложить сумму кубов двух чисел на произведение двух выражений: суммы этих чисел и специального многочлена.
Пример: x3+8=(x+2)(x2−2x+4)
Графическая иллюстрация:
Представьте сложение объёмов двух кубов и их объединение в более сложную геометрическую форму, которая можно разложить на сумму произведений.
7. Разность кубов:
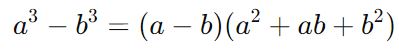
Аналогично сумме кубов, разность кубов раскладывается на произведение разности чисел и специального многочлена.
Пример: x3−27=(x−3)(x2+3x+9)
Графическая иллюстрация:
Если представить разницу объёмов двух кубов, то эта формула описывает разложение этого объёма на части, аналогичные разности и сумме элементов.
Примеры использования формул сокращённого умножения:
1. Факторизация выражений:
Пример: 4x2−25y2=(2x−5y)(2x+5y) (используя разность квадратов).
2. Упрощение многочленов:
Пример: (2x+3)2=4x2+12x+9 (квадрат суммы).
3. Решение уравнений:
Пример: x2−16=0 → (x−4)(x+4)=0, откуда x=4x = 4 или x=−4x = -4.
Как правильно использовать эти формулы:
1. Знание структур: Внимательно определяйте, когда можно применить конкретную формулу. Например, разность квадратов применяется только тогда, когда выражение имеет форму a2−b2.
2. Применение к реальным задачам: Эти формулы помогают решать квадратные и кубические уравнения, факторизовать выражения и ускорять вычисления при работе с многочленами.
3. Практика: Регулярно тренируйтесь на примерах, чтобы формулы стали интуитивно понятными и легко применяемыми.
