Доказательство теоремы Пифагора — одно из самых известных и важных доказательств в геометрии. Теорема утверждает, что для любого прямоугольного треугольника квадрат длины гипотенузы равен сумме квадратов длин катетов:
![]()
где a и b — длины катетов, а c — длина гипотенузы.
Геометрическое доказательство (через квадраты)
1. Построим квадрат со стороной a+b.
Внутри этого квадрата нарисуем четыре копии нашего прямоугольного треугольника, гипотенуза каждого из которых равна c.
Эти четыре треугольника расположим таким образом, чтобы их гипотенузы образовали внутренний квадрат со стороной c, а остальная площадь квадрата состояла из четырёх треугольников. 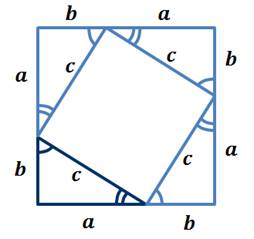
2. Площадь внешнего квадрата равна (a+b)2.
3. Площадь внутреннего квадрата (образованного гипотенузами) равна c2.
4. Площадь четырёх треугольников равна 4⋅(1/2)⋅ab=2ab.
5. Теперь выразим площадь внешнего квадрата двумя способами:
⇒ Как площадь внутреннего квадрата плюс площадь четырёх треугольников:
(a+b)2=c2+2ab
⇒ Как развернутое выражение для (a+b)2:
(a+b)2=a2+2ab+b2
6. Сравниваем эти два выражения:
a2+2ab+b2=c2+2ab
7. Убираем 2ab с обеих сторон:
a2+b2=c2
Таким образом, теорема Пифагора доказана.
Для проверки решений задач с использованием формулы теоремы Пифагора используйте онлайн калькулятор для теоремы Пифагора.
