Бесконечные периодические дроби

Бесконечные периодические десятичные дроби – это дроби, у которых одна цифра или группа цифр повторяются.
Примеры: 0,66666666666666…; 0,33333333333333…; 0,68181818181818…

Повторяющаяся группа цифр называется периодом и записывается в скобках.
Примеры: 0,(6); 0,(3); 0,6(81).

Получить периодическую дробь можно тогда, когда при делении числителя на знаменатель получаются повторяющиеся остатки. Именно повторяющиеся остатки делают процесс деления бесконечным, что приводит к появлению бесконечной периодической дроби.

Пример 1.  Разделить 1 на 3: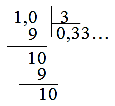
При делении мы постоянно получаем остаток 1, затем приписываем к нему 0 и делим 10 на 3. Эта операция повторяется снова и снова. В результате мы каждый раз получаем повторяющиеся остатки. Поэтому деление 1 на 3 будет выполняться бесконечно. В результате этого образуется бесконечная десятичная дробь.

• Записывается. Обычно бесконечные периодические дроби записывают сокращенно: сначала записывают целую часть, затем ставят запятую и в скобках указывают период (цифру, которая повторяется).
• Читается. Бесконечные периодические дроби читаются так:  «ноль целых и три в периоде»

Пример 2.  Разделить 5 на 11:
При делении мы постоянно получаем остаток 5 или 6. Затем приписываем к остатку 0 и делим 50 или 60 на 11. В результате мы получаем повторяющиеся остатки, поэтому деление 5 на 11 будет выполняться бесконечно.
Записывается: 0,(45).
Читается:  «ноль целых и сорок пять в периоде»

Виды периодических дробей

Периодические дроби бывают двух видов: чистые и смешанные.

⭢ Чистые — дроби, у которых период начинается сразу после запятой.
Примеры: 0,(3); 0,(5); 0,(6).

⭢ Смешанные — дроби, у которых период начинается после некоторого количества не повторяющихся цифр.
Примеры: 0,52(3); 0,16(5); 0,31(6)

Чтобы  записать периодическую дробь в виде десятичной дроби, нужно округлить эту дробь до нужного разряда. Как округлять, можно прочитать в статье «Правила округления чисел«

Примеры округления:
Округлить 0,(3) до сотых. Получаем 0,333333…≈ 0,33.
Округлить 6,31(6) до тысячных. Получаем 6,31666666… ≈ 6,317

Перевод периодической дроби в обыкновенную

✅  Для чистой периодической дроби

Чтобы перевести чистую периодическую дробь в обыкновенную дробь, нужно
➤  в числитель обыкновенной дроби записать период периодической дроби, 
➤  в знаменатель обыкновенной дроби записать некоторое количество девяток, при этом, количество девяток должно быть равно количеству цифр в периоде периодической дроби.

Пример 1: перевести 0,(3) в обыкновенную дробь.
В периодической дроби 0,(3) период состоит из одной цифры 3, поэтому в числителе записываем одну тройку, а в знаменателе — одну девятку.  Полученную дробь  можно сократить на 3, тогда получим обыкновенную дробь 1/3.

Пример 2. Перевести  0,(45) в обыкновенную дробь.
В периодической дроби 0,(45) период состоит из двух цифр, поэтому в числителе записываем 45, а в знаменателе — 99.  Полученную дробь  можно сократить на 9, тогда получим обыкновенную дробь 5/11.

✅  Для смешанной периодической дроби

 Чтобы перевести смешанную периодическую дробь в обыкновенную дробь, нужно
➤  в числителе записать разность:
уменьшаемое — все цифры, стоящие после запятой, в том числе в периоде,
вычитаемое — цифры, стоящие между запятой и первым периодом периодической дроби.
➤  в знаменателе записать некоторое количество девяток и нулей.
количество девяток должно быть равно количеству цифр в периоде периодической дроби,
количество нулей должно быть равно количеству цифр между запятой и периодом периодической дроби.

Пример 3: перевести 0,31(6) в обыкновенную дробь.
➤  В числителе запишем разность разность:
уменьшаемое —  все цифры, стоящие после запятой, включая и период = 316
вычитаемое — цифры, стоящие между запятой и периодом = 31
получаем числитель = (316-31).
➤  В знаменателе запишем некоторое количество девяток и нулей.
количество девяток равно количеству цифр в периоде периодической дроби 0,31(6) — одна девятка
количество нулей равно количеству цифр между запятой и периодом — два нуля.
получаем знаменатель = 900. Получили дробь, которую можно сократить.

Пример 4. перевести 0,72(62) в обыкновенную дробь.
➤  В числителе: уменьшаемое = 7262, вычитаемое = 72, получаем числитель = (7262-72).
➤  В знаменателе:  2 цифры в периоде (99), две цифры между запятой и периодом (00), получаем 9900.
Получили дробь, которую можно сократить.