Равноускоренное движение: определение и формулы

Прямолинейное равноускоренное движение — это прямолинейное движение, при котором скорость тела изменяется (увеличивается или уменьшается) на одну и ту же величину за равные промежутки времени.

Ускорение — физическая величина, характеризующая быстроту изменения скорости тела. То есть, показывает, на какую величину изменяется скорость за единицу времени.

Примеры равноускоренного движения:

разгон самолета перед взлетом;
падающая с крыши сосулька;
торможение лыжника на горном склоне;
разгоняющийся на склоне сноубордист;
свободное падение в результате прыжка с парашютом;
камень брошенный под углом к горизонту;

Равномерное прямолинейное движение является частным случаем равноускоренного движения, при котором ускорение равно нулю.

Равноускоренное движение: формулы

Формула для скорости при равноускоренном движении:

V_к=V_н+at

где: V_к — конечная скорость тела,
V_н — начальная скорость тела,
a=const — ускорение (a>0 при ускорении, a<0 при замедлении)
t — время.

Формула для ускорения при равноускоренном движении:

a=(V_к-V_н)/t

Во время движения тела ускорение остается постоянным.

Задача 1

Кирилл ехал на велосипеде со скоростью 6 м/с, затем начал разгоняться на горке. Чему будет равна его скорость через 10 секунд, если ускорение равно 0,5 м/с?
Решение. Vн=6м/с, ускорение a=0,5м/с, время разгона t=10 секунд.
Получаем: Vн= 6 + 0,5 · 10 = 11 м/с.
Ответ: за 10с Кирилл разгонится до скорости 11 м/с.

Формула расстояния при равноускоренном движении

Если известны время, скорость начальная и скорость конечная

S = t*(V_н+ V_к)/2

Если известны время, скорость начальная и ускорение

S = V_нt + at²/2 **= t*(V_н + at/2)**

где: S — путь, пройденный за время t,
Vн — начальная скорость,
Vк — конечная скорость,
a — ускорение тела,
t — время.

В случае равноускоренного движения с неизвестным временем движения, но с заданными начальной и конечной скоростями пройденный путь можно найти с помощью следующей формулы:

2аS = V_к²−V_н²

где S — путь, пройденный за время t ,
V0 — начальная скорость,
V — скорость в момент времени t,
a — ускорение тела.

Задача 2

Таксист получил заказ и начал движение с ускорением 0,1 м/с2. На каком расстоянии от начала движения его скорость станет равной 15м/с?
Решение. Так как таксист начал движение, начальная скорость равна нулю (Vн=0), Vк=15м/с, ускорение a=0,1м/с2.
Получаем:
S = 15^2 — 0^2 =1125 м.
Ответ: на расстоянии 1 125 м от начала движения скорость такси станет равной 15 м/с.

Перемещение при равноускоренном движении

Важно напомнить разницу между путем и перемещением тела.

Путь — длина траектории. Если тело движется в любом направлении, то его путь увеличивается. Путь — всегда положительное значение.
Перемещение — вектор, соединяющий начальное и конечное положение тела. Проекция перемещения может принимать отрицательное значение.

Например, если путник прошел в одну сторону расстояние S1, а обратно — S2, то: путь тела равен S1 + S2, а перемещение равно S1 − S2. В некоторых задачах путь и перемещение могут совпадать, но не всегда.

Равноускоренное движение: графически

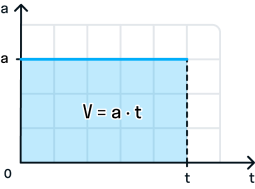
График зависимости ускорения от времени:
Во время движения тела ускорение остается постоянным.

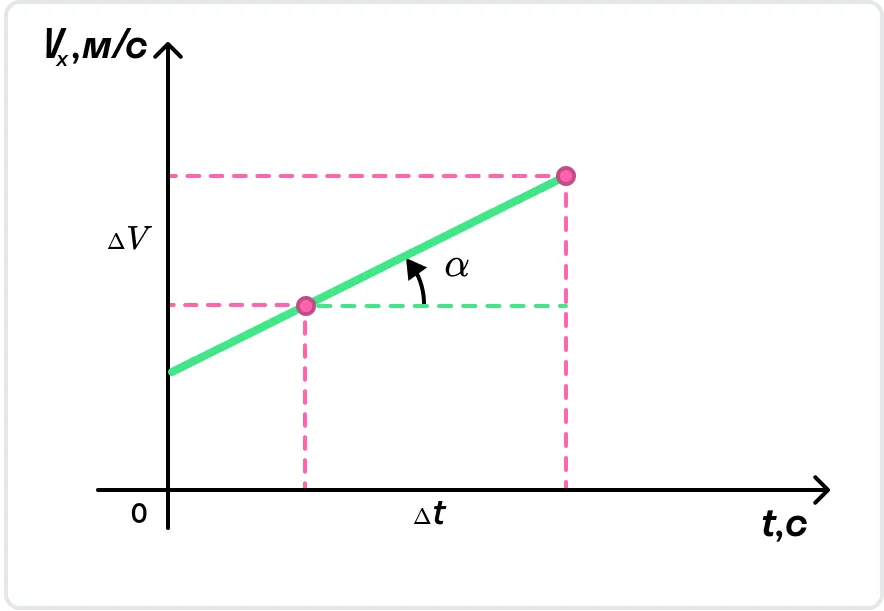
Взаимосвязь скорости, времени и расстояния:
На рисунке показан график, в котором скорость равномерно увеличивается.
С помощью графика скорости можно определить ускорение тела как тангенс угла наклона графика к оси времени.

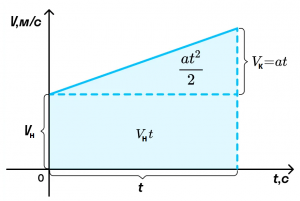
Из графика скорости получим формулу пути при равноускоренном движении тела.

Пройденный телом путь при равноускоренном движении численно равен площади фигуры под графиком зависимости скорости от времени. Вычислим площадь трапеции как сумму площадей прямоугольника V_нt и треугольника at²/2. Получим: S = V_нt + at²/2.

Математически зависимость координаты от времени при равноускоренном движении представляет собой квадратичную функцию, ее график — парабола.

Задача 3

Лыжник подъехал со скоростью 3 м/с к спуску длиной 36 м и съехал с него за несколько секунд, при этом его конечная скорость составила 15 м/с. Определите местонахождение лыжника спустя 2с после начала движения из начала координат.

Дано:
Vн = 3 м/с, начальная координата (t) равна нулю,
Vк = 15м/с,
a — скорость лыжника увеличивается, поэтому ускорение — положительное число,
S = 36м — путь с горы,
t — 2с.

Решение:
Найдем ускорение из формулы пути при равноускоренном движении: 2аS = V_к²−V_н²
Получим: а = (V_к²−V_н² )/2S = (225-9)/(2*36) = 3 м/с2.
Составим уравнение движения лыжника исходя из формулы: S = V_нt + at²/2.
Получаем: x(t) = 3t + 1,5t²
По уравнению определим координату лыжника в момент времени t = 2с:
Получаем: x(2) = 3*2 + 1,5*2² =6+6=12 м.

Ответ: через 2 с после начала движения координата лыжника будет равна 12 м.

Для того, чтобы проверить правильность решения задач на равноускоренное движение, воспользуйтесь калькулятором равноускоренного движения.

Для того, чтобы перевести единицы измерения, воспользуйтесь конвертерами единиц измерения: